그림 14-5에서 S=S U {0} 연산을 했습니다. 이제 S에 새롭게 삽입된 정점 0과 adj[0]={1, 2}에 있는 정점 간에 relaxation을 합니다. 정점 1과 정점 2 모두 S에 속하지 않았으므로 relaxation의 대상이 됩니다. adj[0]의 집합 중 S에 속한 정점이 있다면 이는 relaxation의 대상이 아닙니다.

다음은 relaxation을 한 후의 그림입니다.

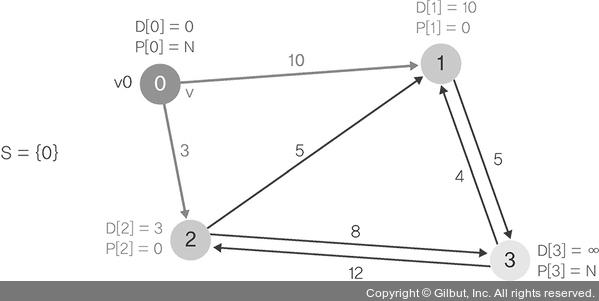
▲ 그림 14-6 데이크스트라 3

그림 14- 6은 adj[0]={1, 2}에 대해 relaxation을 한 후의 그래프를 보여 줍니다. 1, 2 모두 기존 D[1], D[2] 값이 무한대였기 때문에 D[0]+weight(0, 1)과 D[0]+weight(0, 2)로 각각 업데이트됩니다. 이제 최소 우선순위 큐에서 pop을 하면 현재 밝혀진 거리가 가장 짧은 정점이 나옵니다. 정점 2의 D[2] 값이 3으로 가장 작습니다.