2. 편차
학생 A 집단의 몸무게 평균인 66을 각 학생의 몸무게 값에서 빼 보겠습니다.
표 2 | 학생 A 집단의 몸무게 값과 평균 차이
|
이름 |
몸무게 값(A) |
몸무게 평균(B) |
차이(A-B) |
|
최준호 |
74 |
66 |
8 |
|
김주찬 |
66 |
66 |
0 |
|
이상윤 |
61 |
66 |
-5 |
|
이두희 |
59 |
66 |
-7 |
|
최대호 |
70 |
66 |
4 |
각 몸무게 값에서 몸무게 평균인 66을 뺐더니 차이를 구할 수 있었습니다. 이 차이(관측 값-평균값)는 각 값이 평균에서 떨어져 있는 정도라고 말할 수도 있습니다. 이 떨어진 정도를 편차(deviation)라고 합니다. 예를 들어 ‘최준호’ 학생은 평균에서 8만큼, ‘최대호’ 학생은 평균에서 4만큼, ‘이두희’ 학생은 -7만큼 떨어져 있습니다.
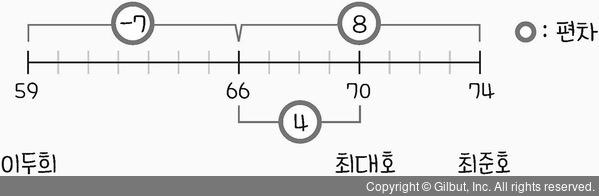
그림 1 | 편차 개념
그런데 각 관측 값의 편차가 서로 달라 한눈에 보기 불편하고(8, 4, -7), 편차의 평균값을 알고 싶어도 편차를 모두 더하면 0이 되기 때문에 평균을 구할 수 없습니다.
8 + 0 + -5 + -7 + 4 = 0
그래서 구하는 것이 분산입니다.