4. 표준편차

분산에 루트를 적용해 보겠습니다.

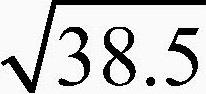= 6.204836822995428

루트를 적용하니 약 6.2가 나왔습니다. 즉, 학생 A 집단의 다섯 명 몸무게는 66을 기준으로 평균 약 6.2 정도 차이가 난다고 말할 수 있습니다. 이처럼 분산 값에 루트를 적용한 값을 표준편차(STandard Deviation, STD)라고 합니다. 지금까지 배운 원리에서 알 수 있듯이, 표준편차가 크다는 것은 집단의 각 값들의 퍼져 있는 정도가 크다는 것이라고 할 수 있습니다. 반대로 작은 경우에는 퍼져 있는 정도가 작다는 의미입니다(비슷한 값이 모여 있음).

지금까지 과정을 다음과 같이 R로 구할 수 있습니다.

weight <- c(74, 66, 61, 59, 70)     # 학생 A 집단의 몸무게
mean(weight)                        # 평균
[1] 66

median(weight)                      # 중앙값(74, 70, 66, 61, 59)의 정중앙 값
[1] 66

var(weight)                         # 분산
[1] 38.5

sd(weight)                          # 표준편차
[1] 6.204837