2.2.1 경사 하강법 최적화 이해하기

간단한 단일 층 모델은 다음과 같은 선형 함수 f(input)을 학습합니다.

output = kernel * input + bias

여기서 커널과 편향은 밀집 층의 조정 가능한 파라미터(가중치)입니다. 이 가중치에는 신경망을 훈련 데이터에 노출시켜 학습시킨 정보가 담겨 있습니다.

초기에 이 가중치는 랜덤한 작은 값으로 채워져 있습니다(랜덤 초기화(random initialization)라고 부릅니다). 물론 커널과 편향이 랜덤할 때 kernel * input + bias가 어떤 유용한 값을 만들 거라 기대하지 못합니다. 상상을 해보면 이 파라미터를 다르게 선택했을 때 MAE 값이 어떻게 변하는지 그릴 수 있습니다. 이 파라미터가 그림 2-4에서 찾은 최적의 직선 기울기와 절편에 가까울 때 손실이 낮을 것으로 기대할 수 있습니다. 파라미터가 이와 동떨어진 직선을 그릴수록 손실이 더 나빠집니다. 손실을 모든 튜닝 가능한 파라미터의 함수로 보는 이런 개념을 손실 표면(loss surface)이라고 합니다.

이 예제는 아주 간단하기 때문에 튜닝 가능한 파라미터가 두 개이고 하나의 타깃을 가지고 있습니다. 따라서 그림 2-5와 같이 손실 표면을 2D 등고선 그래프로 그릴 수 있습니다.⁹ 손실 표면이 매끈한 오목한 그릇 모양이므로 최적의 파라미터 설정을 의미하는 전역 최솟값(global minimum)은 그릇의 바닥에 위치합니다. 하지만 일반적으로 딥러닝 모델의 손실 표면은 이보다 훨씬 더 복잡합니다. 2차원보다 훨씬 많은 차원을 가지고 있고 지역 최솟값(local minima)이 많을 수 있습니다. 지역 최솟값은 전체적으로 가장 낮은 최솟값은 아니지만 주변보다 낮은 지점을 말합니다.

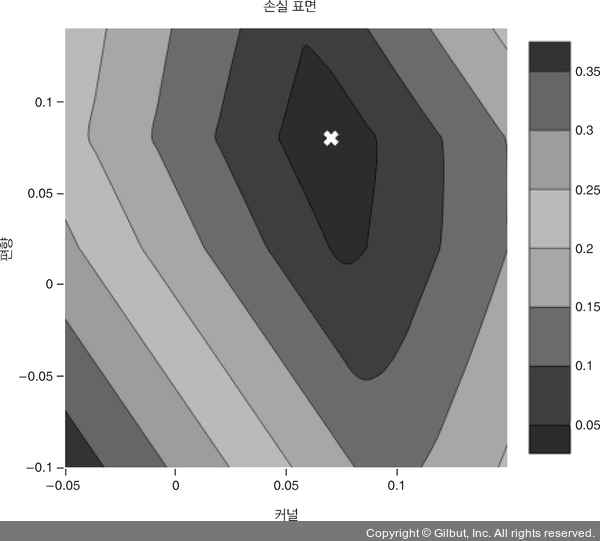
▲ 그림 2-5 손실 표면은 모델의 튜닝 가능한 파라미터에 대한 손실을 그린 등고선 그래프. 이 그래프를 보면 (하얀 X 표시가 된) {bias: 0.08, kernel: 0.07} 지점이 낮은 손실을 위한 합리적인 선택 같다. 이런 지도를 만들기 위해 모든 파라미터 값을 테스트하기는 어렵지만, 만약 그렇게 한다면 최적화는 매우 간단하다. 그냥 가장 낮은 손실에 해당하는 파라미터를 선택하면 된다!