3.1.1 신경망의 비선형성에 대한 직관 기르기

왜 정확도가 향상되었을까요? 그림 3-1에서 볼 수 있듯이 모델의 복잡도가 향상되었기 때문입니다. 첫째, 뉴런의 층이 추가되었습니다. 이 층이 은닉층입니다. 둘째, 은닉층이 (코드에서 activation: 'sigmoid'로 지정된) 비선형 활성화 함수(activation function)를 가지고 있습니다. 활성화 함수는 그림 3-1의 B에서 네모 상자로 표시되어 있습니다. 활성화 함수⁴는 원소별 변환입니다. 시그모이드(sigmoid) 함수는 음의 무한대에서 양의 무한대까지 모든 실수 값을 아주 작은 범위(여기서는 0에서 1까지)로 줄인다는 점에서 일종의 압축 비선형 함수입니다. 이 함수의 수학 공식과 그래프가 그림 3-2에 나타나 있습니다. 밀집 은닉층을 예로 들어 보죠. 행렬 곱셈과 편향을 더한 결과가 다음과 같은 랜덤한 배열로 구성된 2D 텐서라고 가정해 보겠습니다.

[[1.0], [0.5], ..., [0.0]],

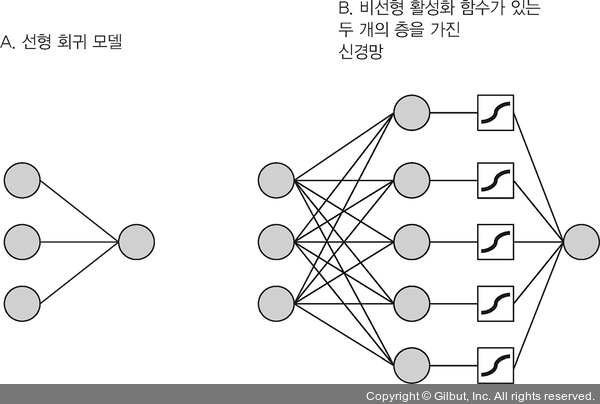
▲ 그림 3-1 보스턴 주택 데이터셋을 위해 만든 선형 회귀 모델(A)과 두 개의 층을 가진 신경망(B). 간단하게 나타내기 위해 입력 특성의 개수를 12개에서 세 개로 줄이고 B에서 은닉층의 유닛 개수를 50개에서 다섯 개로 줄였다. 두 모델은 모두 (하나의 타깃 값을 가진) 단변량(univariate) 회귀 문제를 풀기 때문에 하나의 출력 유닛만 가지고 있다. B는 모델의 은닉층에 비선형 (시그모이드) 활성화 함수를 사용하는 예다.