③ 피보나치 수열

피보나치 수열은 첫째와 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열(처음 여섯 항은 각각 1, 1, 2, 3, 5, 8)이며, 이 수열의 항들은 피보나치 수라 부른다. 일반항은 레온하르트 오일러가 1765년에 처음 발표했으나 잊혔고, 1848년에 자크 비네에 의해 재발표되었다. 그 식은 다음과 같다.

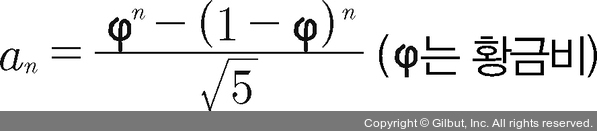
피보나치 수가 처음 언급된 문헌은 기원전 5세기 인도의 수학자 핑갈라가 쓴 책이다. 7세기경에 활동한 인도 수학자 비라한카의 저서에서도 피보나치 수가 등장한다.

현대에 피보나치 수열은 컴퓨터 과학에서 자료 구조와 알고리즘의 최적화, 생물학에서 식물 성장의 동역학, 금융공학에서 주식 시장의 움직임을 설명하는 엘리어트 파동 이론 등 다양한 분야에서 광범위하게 활용되고 있다.