꺾은선(lines)

lines( )는 points( )와 마찬가지로 plot( )으로 새로운 그래프가 시작된 뒤 그 위에 꺾은선을 추가하여 그리는 목적으로 사용한다. 꺾은선은 시계열 데이터에서 추세를 표현하거나, 여러 범주의 데이터를 서로 다른 색상 또는 선 유형으로 표현하는 데 사용한다.

lines(
  x,      # X 좌표
  y=NULL, # Y 좌표
  ...     # 추가적인 그래픽 파라미터
)

다음은 [0, 2π] 구간에 대해 사인sine 함수 그래프를 그리는 예다.

> x <- seq(0, 2*pi, 0.1)
> y <- sin(x)
> plot(x, y, cex=.5, col="red")
> lines(x, y)

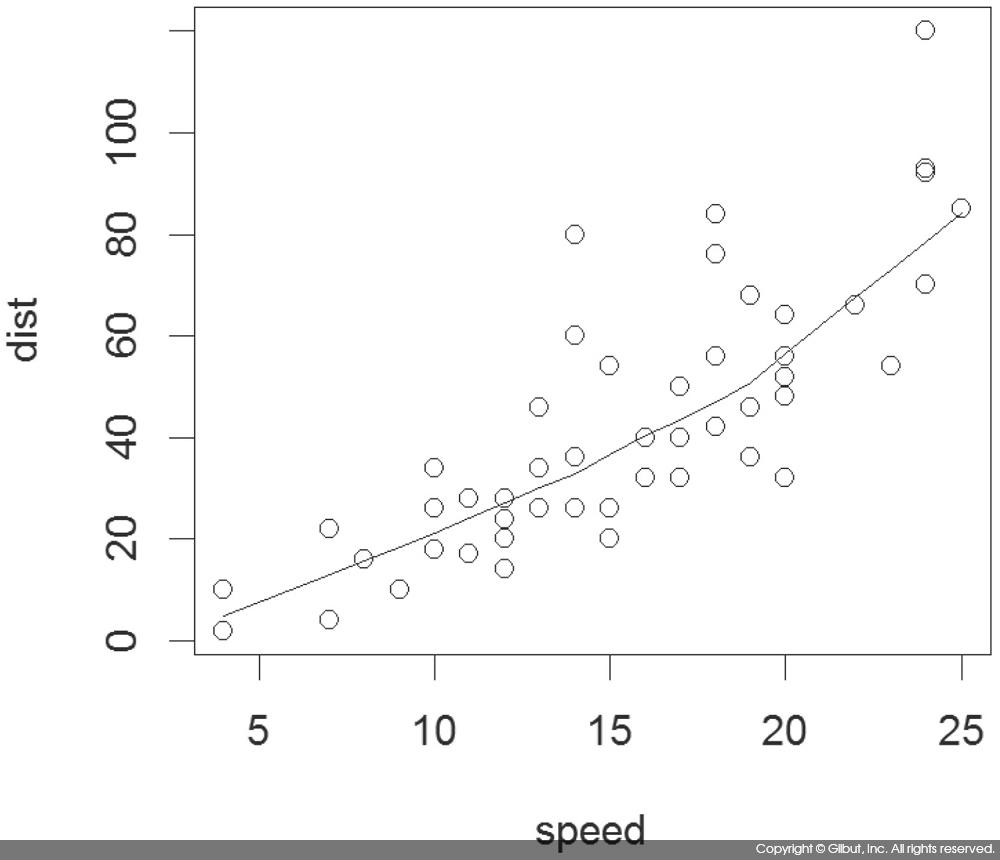
또 다른 예로 example(lines)를 입력하면 cars 데이터에 LOWESS를 적용한 예를 볼 수 있다. LOWESS는 데이터를 설명하는 일종의 추세선을 찾는 방법이다. LOWESS는 데이터의 각 점을 y, 각 점의 주변에 위치한 점들을 x라고 할 때 했을 때, y를 x로부터 추정하는 다항식을 찾는다. LOWESS가 찾는 다항식은 y = ax +b 또는 y = ax² + bx + c와 같은 형태의 저차 다항식low degree polynomial이다. 다항식을 찾을 때는 추정하고자 하는 y에 가까운 x일수록 더 큰 가중치를 준다. 이런 이유로 LOWESS는 지역 가중 다항식 회귀3 Locally Weighted Polynomial Regression라고도 부르며, 그 결과는 각 점을 그 주변 점들로 설명하는 다항식들이 연결된 모양이 된다. 이렇게 각 점에서 찾아진 다항식들을 부드럽게 연결하면 데이터의 추세를 보여주는 선이 된다. 자세한 내용은 참고자료 [1]을 보기 바란다.

cars 데이터에 대해 LOWESS를 수행해보자. cars 데이터는 자동차의 속도와 그 속도에서의 제동 거리를 담고 있는 데이터다.

> data(cars)
> head(cars)
  speed dist
1     4    2
2     4   10
3     7    4
4     7   22
5     8   16
6     9   10

각각의 관측값을 점으로 표시하고, LOWESS를 수행한 결과를 보이는 코드는 다음과 같다.

> plot(cars)
> lines(lowess(cars))

3 회귀 분석(Regression Analysis)이란 변수 간의 관계를 조사하는 통계적 기법을 뜻한다. 예를 들어, 키와 몸무게 사이의 상관관계를 height=a×weight+b와 같은 수식으로 찾는 것이 회귀 분석이다.

4 비모수적(non-parameteric)이라 함은 특정한 분포를 가정하지 않으며 고정된 모델을 가정하지 않는 통계적 기법을 뜻한다. http://en.wikipedia.org/wiki/Non-parametric_statistics를 참고하기 바란다.