직선(abline)

abline( )은 y = ax + b 형태의 직선이나 y=h 형태의 가로로 그은 직선 또는 x=v 형태의 세로로 그은 직선을 그래프에 그린다. abline( )이 그리는 것은 꺾이지 않고 그어진 일직선이다. 따라서 lines( )가 주어진 (x, y) 좌표들을 연결하는 꺾은선을 긋는 것과는 차이가 있다.

abline(
  # a, b는 y = a + bx 형태의 직선을 그릴 때 절편과 기울기
  a=NULL,
  b=NULL,
  h=NULL,   # y=h 형태의 수평선을 그릴 때 지정
  v=NULL,   # x=v 형태의 수직선을 그릴 때 지정
  reg=NULL, # 선형 회귀 모델을 그릴 때 지정
  ...
)

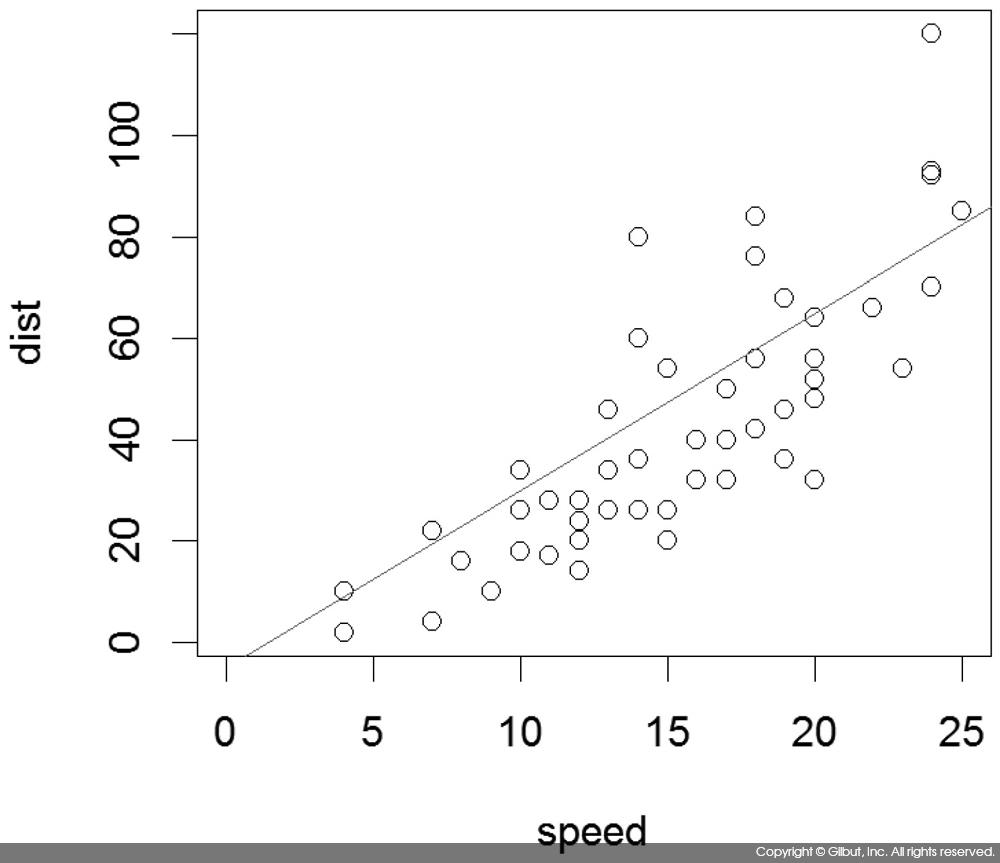
cars 데이터에서 제동 거리와 속도가 dist = -5 + 3.5 × speed로 근사될 수 있다고 가정해보자. 그러면 다음과 같이 abline( )을 사용하여 근사가 얼마나 잘 이루어지는지를 시각화할 수 있다.

> plot(cars, xlim=c(0, 25))
> abline(a=-5, b=3.5, col="red")

이 그래프에 speed와 dist의 평균까지 표시해보자. 다음 코드에서 lty는 선의 유형을 지정하는 데 사용하며, 2는 대시 선dashed line5 을 뜻한다.

> plot(cars, xlim=c(0, 25))
> abline(a=-5, b=3.5, col="red")
> abline(h=mean(cars$dist), lty=2)
> abline(v=mean(cars$speed), lty=2)

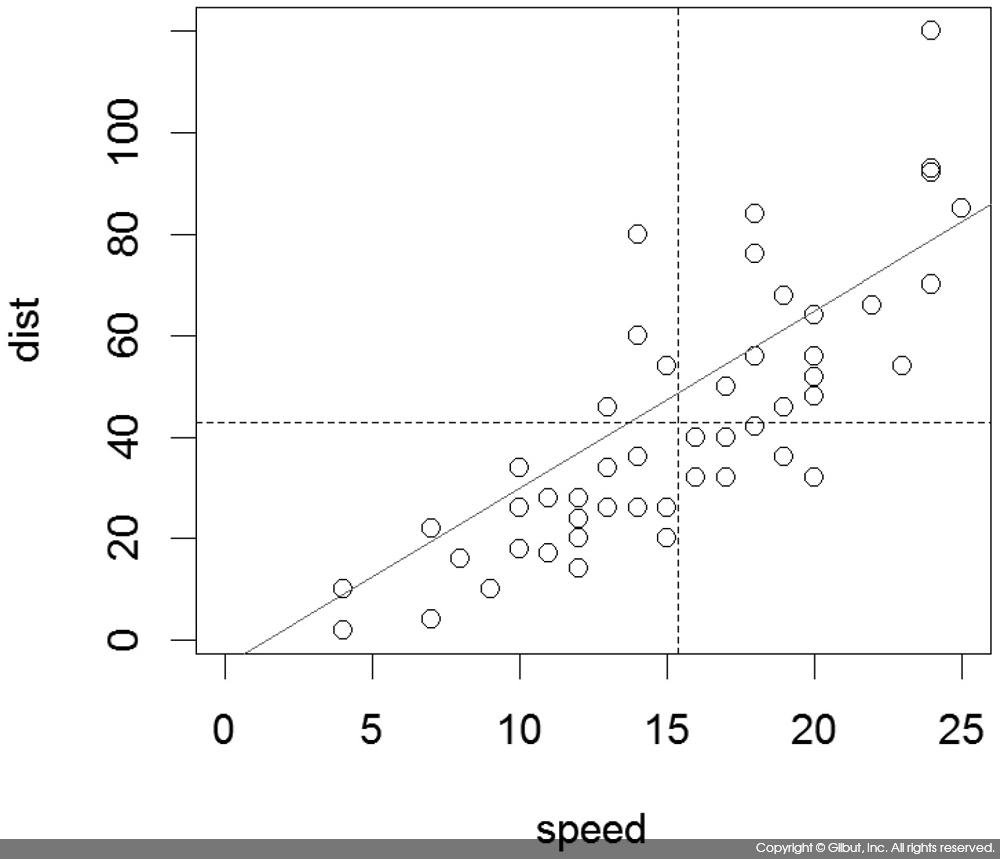
그래프를 그려본 결과 dist = -5 + 3.5 × speed는 (x = speed의 평균, y = dist의 평균) 점을 지나지 않는다. 따라서 이 직선은 올바른 선형 회귀 직선은 아니다.[2]

5 ‘6.2.8 선 유형(lty)’ 절에서 lty에 대해 설명했다.