다각형(polygon)

polygon( )은 다각형을 그리는 데 사용하는 함수다.

polygon(
  x,       # 다각형의 X 좌표
  y=NULL,  # 다각형의 Y 좌표
  ...
)

polygon( )의 예로 cars 데이터에 선형 회귀를 수행하고 신뢰 구간confidence interval을 polygon( ) 함수를 사용해 그려보는 조금은 복잡하지만 실제적인 예를 살펴보자.

선형 회귀는 종속 변수 y를 하나 또는 그 이상의 설명 변수 X6 로 설명하는 모델을 만드는 방법이다. 선형 회귀가 찾은 결과는 y = ax + ε과 같은 모양이 된다. 선형 회귀는 lm( )과 predict( )를 사용해 수행할 수 있다.

lm(
  formula,  # 종속 변수 ~ 설명 변수
  data      # 포뮬러에 따라 선형 모델을 만들 데이터
)

predict.lm(
  object,   # 선형 모델 객체
  newdata,  # 예측을 수행할 새로운 데이터
            # 이 값을 생략하면 선형 모델을 만들 때 사용한 데이터가 사용된다.
  # 구간 정보인 none, confidence, prediction은 각각 신뢰 구간을 계산하지 않음, 신뢰 구간,
  # 예측 구간을 뜻한다. 신뢰 구간은 X = x0 값이 주어졌을 때 종속 변수 y의 기댓값의 구간을 뜻한다.
  # 예측 구간은 X=x0인 X가 있을 때 개별 Y의 구간을 뜻한다.
  interval=c("none", "confidence", "prediction")
)

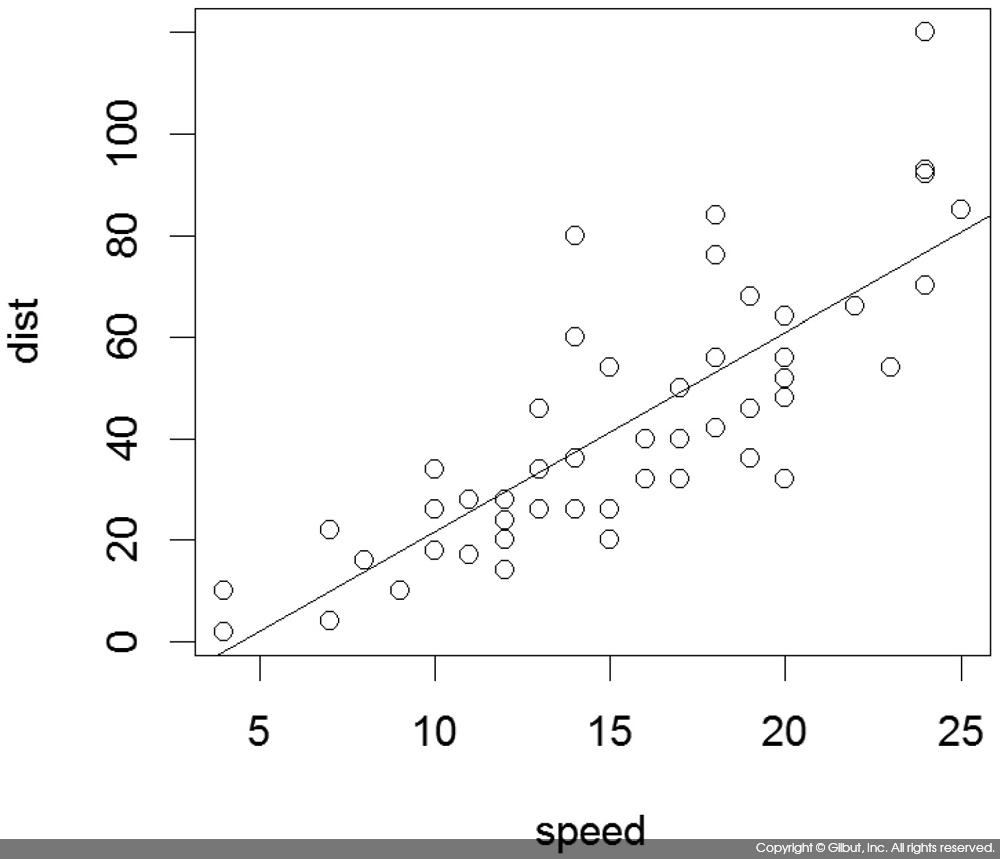
cars에 대한 선형 회귀를 수행해보자. lm( )에서 포뮬러는 dist로 주어졌는데, 이는 dist = a + b × speed + ε의 모델을 의미한다. 수식에서 a는 절편, b는 기울기, ε은 dist와 a + b × speed 사이의 차, 즉 오차를 뜻한다.

> (m <- lm(dist ~ speed, data=cars))
Call:
lm(formula = dist ~ speed, data = cars)

Coefficients:
(Intercept)     speed
    -17.579     3.932

회귀 모델(모형)을 적합한 결과 dist = -17.579 + 3.932 × speed + ε의 식이 얻어졌다. 앞에서도 설명했듯이 lm( )으로 만든 모델은 단순히 abline( ) 함수에 넘겨주는 것만으로 그래프에 표시할 수 있다.

> plot(cars)
> abline(m)  # abline()의 reg 인자에 선형 회귀 모델 m이 지정됨

6 소문자 x가 아니라 대문자 X를 사용했다는 점에 유의하자. 대문자 X는 벡터 또는 행렬을 의미한다.