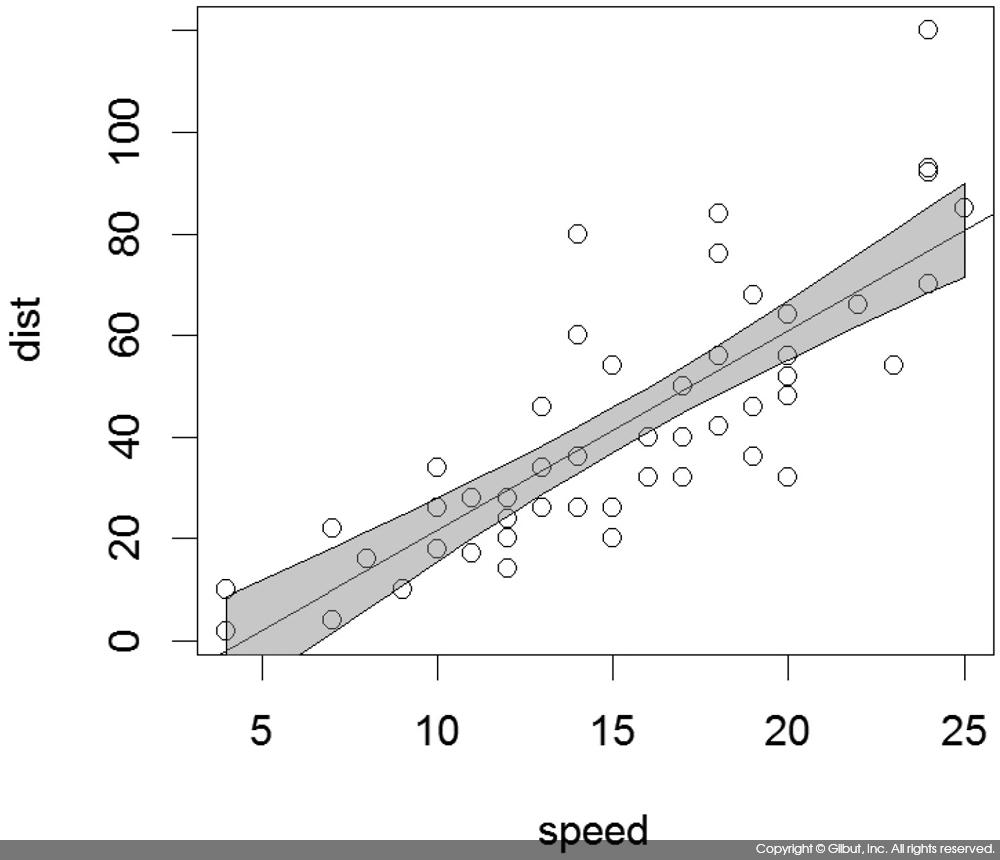
선형 회귀 모델이 주어졌을 때 새로운 데이터에 대한 예측은 predict( )로 수행한다. 함수 호출 시 인자로 interval=“confidence”를 지정해 신뢰 구간까지 구해보자.

> p <- predict(m, interval="confidence")
> head(p)
        fit        lwr       upr
1 -1.849460 -12.329543  8.630624
2 -1.849460 -12.329543  8.630624
3  9.947766   1.678977 18.216556
4  9.947766   1.678977 18.216556
5 13.880175   6.307527 21.452823
6 17.812584  10.905120 24.720047

위의 코드에서 예측 결과를 저장한 p의 데이터 타입은 행렬matrix이며, fit는 회귀 모델로 적합된 y 값, lwr은 신뢰 구간의 하한, upr은 신뢰 구간의 상한을 뜻한다. p의 각 행은 cars의 각 행에 대응한다. 예를 들어, p의 첫 행에 있는 fit 값 -1.849460은 cars의 첫 행에 있는 speed 값 4에 대한 dist 예측값이다.

polygon( )으로 신뢰 구간을 그리려면 그래프에 그릴 다각형의 x 좌표, y 좌표를 구해야 한다. 이는 cars의 speed를 x 좌표, 앞서 코드에서 구한 p의 lwr과 upr을 각각 y 좌표로 한 점들을 나열해 구할 수 있다. 단, 닫혀 있는 다각형을 그려야 하므로 시작점과 끝점이 만나야 한다는 점에 유의한다. 이를 표현한 코드는 다음과 같다.

> x <- c(cars$speed,
+        tail(cars$speed, 1),
+        rev(cars$speed),
+        cars$speed[1])

> y <- c(p[, "lwr"],
+        tail(p[, "upr"], 1),
+        rev(p[, "upr"]),
+        p[, "lwr"][1])

이 코드는 다음과 같이 이해할 수 있다. 먼저 (cars$speed, p[, “lwr”])의 좌표들을 나열한다. 그러면 하한에 대한 선이 완성된다. 다음으로 (cars$speed의 가장 마지막 값, p[, “upr”]의 가장 마지막 값)으로 선을 그린다. 이때 사용한 tail( )은 head( )의 반대 기능을 하는 함수로, 데이터의 가장 마지막 값을 얻어오는 데 사용했다. 이제 (cars$speed, p[, “upr”])의 점들을 따라 선을 그리되 그래프의 우측에서 좌측으로 그려나간다. 이는 rev( ) 함수를 사용해 수행한다. 마지막으로 시작점인 (cars$speed의 첫 번째 값, p[, “lwr”]의 첫 번째 값)으로 선을 그려 도형을 닫는다.

신뢰 구간을 그래프에 그리는 것이므로, 이 영역을 회색으로 색칠하는 것이 보기에 좋을 것이다. 그러나 col=“grey”와 같이 색을 지정하면 polygon( ) 호출 이전에 그래프에 그려진 내용이 모두 가려져버린다. 따라서 rgb( ) 함수에 알파alpha 값을 지정해 투명한 색을 사용한다.

전체 코드를 살펴보자.

> m <- lm(dist ~ speed, data=cars)
> p <- predict(m, interval="confidence")
> x <- c(cars$speed,
+        tail(cars$speed, 1),
+        rev(cars$speed),
+        cars$speed[1])
> y <- c(p[, "lwr"],
+        tail(p[, "upr"], 1),
+        rev(p[, "upr"]),
+        p[, "lwr"][1])
> plot(cars)
> abline(m)
> polygon(x, y, col=rgb(.7, .7, .7, .5))