상자 그림(boxplot)

상자 그림은 데이터의 분포를 보여주는 그림으로 가운데 상자는 제1사분위수, 중앙값, 제3사분위수9를 보여준다. 상자의 좌우 또는 상하로 뻗어나간 선(whisker라고 부름)은 ‘중앙값 - 1.5 × IQR’보다 큰 데이터 중 가장 작은 값(lower whisker라고 부름), ‘중앙값 + 1.5 × IQR’보다 작은 데이터 중 가장 큰 값upper whisker을 각각 보여준다. IQR은 ‘Inter Quartile Range’의 약어로 ‘제3사분위수 – 제1사분위수’로 계산한다. 그래프에 보이는 점들은 이상치outlier에 해당하는데, lower whisker보다 작은 데이터 또는 upper whisker보다 큰 데이터가 이에 해당한다.

boxplot(
  x # 상자 그림을 그릴 데이터
)

boxplot(
  formula, # y ~ grp의 형식으로 y는 분포를 그릴 값, grp는 값들을 그룹 짓는 변수다.
           # 결국 y ~ grp는 y에 대한 상자 그림을 grp마다 그린다.
  data=NULL,        # 포뮬러가 적용될 데이터 프레임(또는 리스트)
  horizontal=FALSE, # TRUE면 세로로, FALSE면 가로로 상자 그림을 그린다.
  # TRUE면 중앙값에 대한 일종의 신뢰 구간을 표시하는 움푹 들어간 구간을 그린다. 만약 두 개의
  # 상자 그림에 notch=TRUE를 지정해 그린 다음 두 그래프의 움푹 들어간 구간이 서로 겹치지
  # 않으면 이는 두 데이터의 중앙값이 서로 다르다는 강한 증거가 된다.
  notch=FALSE,
  ...
)

다음은 iris$Sepal.Width에 대해 상자 그림을 그리는 예다.

> boxplot(iris$Sepal.Width)

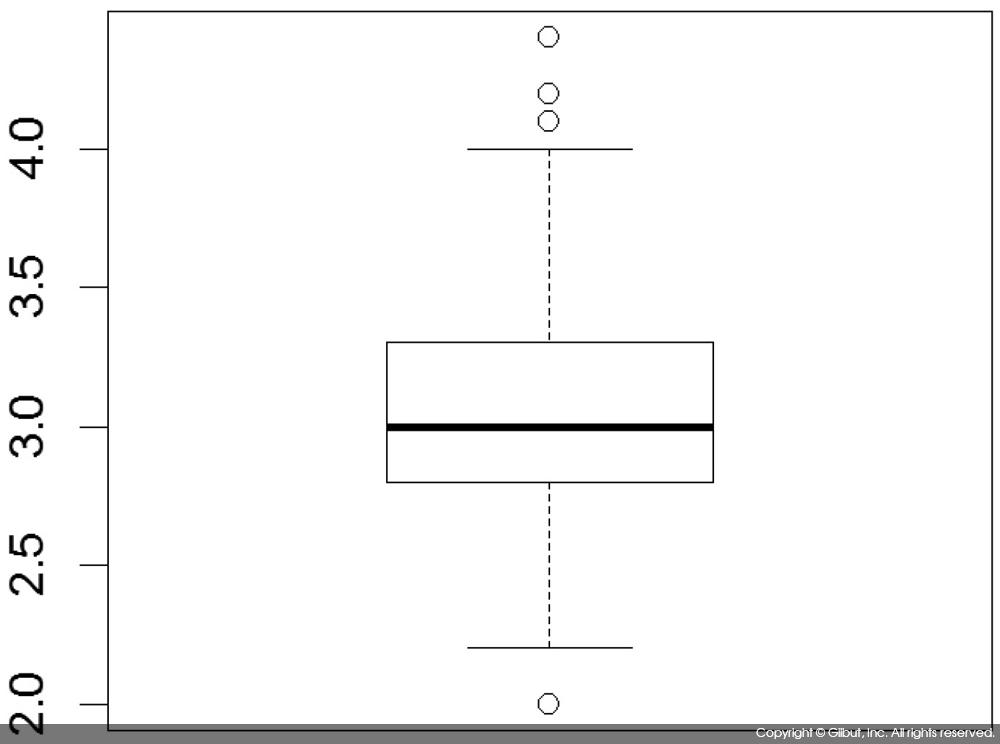
그림에서 제1사분위수는 약 2.8, 중앙값은 약 3.0, 제3사분위수는 약 3.3 정도로 나타났다. lower whisker는 약 2.2였고, lower whisker보다 작은 이상치는 1개 발견되었다. 마찬가지로 upper whisker는 약 4.0이었고 이 값보다 큰 이상치는 3개였다.

상자 그림에 표시된 이러한 값들을 정확히 확인하려면 boxplot( )의 반환 값을 보면 된다. 도움말 ?boxplot의 ‘Value’ 항목을 보면 boxplot( )의 반환 값은 리스트로, stats는 (lower whisker, lower hinge, 중앙값, upper hinge, upper whisker)10 를 포함하고 있고, out은 outlier를 저장하고 있다. iris$Sepal.Width에 대해 이 값들을 살펴보자.

> (boxstats <- boxplot(iris$Sepal.Width))
$stats
     [,1]
[1,]  2.2
[2,]  2.8
[3,]  3.0
[4,]  3.3
[5,]  4.0

$n
[1]  150

$conf

         [,1]
[1,] 2.935497
[2,] 3.064503

$out
[1] 4.4 4.1 4.2 2.0

$group
[1] 1 1 1 1

$names
[1] "1"

lower whisker는 2.2, lower hinge는 2.8, 중앙값은 3.0, upper hinge는 3.3, upper whisker는 4.0이었다. outlier는 4.4, 4.1, 4.2, 2.0이었다(그 외 값의 의미는 도움말을 참고하기 바란다).

이 정보를 사용해 앞서 보인 iris의 outlier 옆에 데이터 값을 표시해보자.

> boxstats <- boxplot(iris$Sepal.Width, horizontal=TRUE)
> text(boxstats$out, rep(1, NROW(boxstats$out)), labels=boxstats$out, pos=c(1, 1, 3, 1))

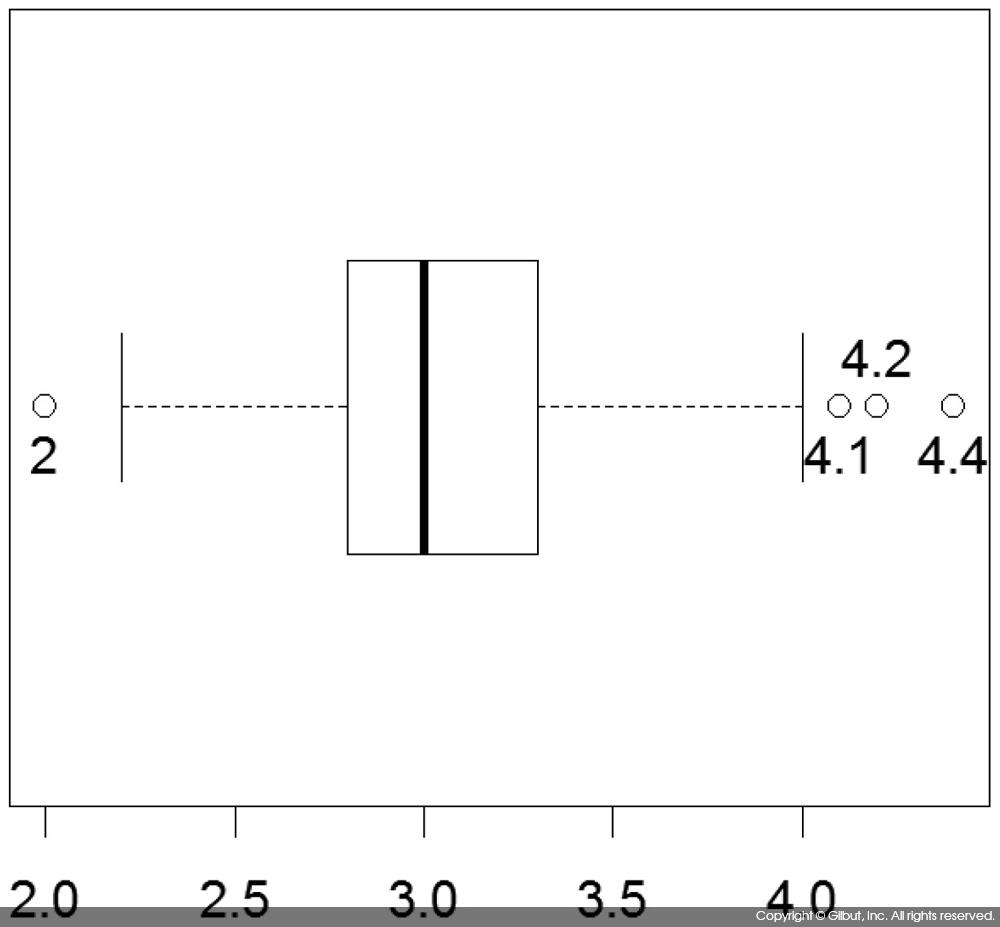
boxplot( ) 호출 시 지정한 horizontal=TRUE는 상자 그림을 가로로 그리게 한다. text( )를 호출할 때 y 좌표는 rep(1, NROW(boxstats$out)을 사용했는데, 이 값은 boxstats$out의 길이가 4므로 1이 4회 반복된 벡터인 c(1, 1, 1, 1)이 된다. 즉, 문자열의 위치를 (outlier 값, 1)로 잡은 것이다. pos=c(1, 1, 3, 1)은 문자열을 점의 하단, 하단, 상단, 하단에 표시하라는 의미다.

9 데이터를 크기 순서로 늘어놓았을 때 25%에 해당하는 값을 제1사분위수, 50%에 해당하는 값을 중앙값(median), 75%에 해당하는 값을 제3사분위수라 한다.

10 lower hinge, upper hinge는 제1사분위수, 제3사분위수와 유사하면서도 다소 계산 방법이 다른 값이다. 지금은 이들이 각각 제1사분위수, 제3사분위수라고 생각해도 무방하다. 이들의 차이는 ‘7.2.2 다섯 수치 요약’ 절에서 다시 다룬다.