boxplot( )에는 또 한 가지 흥미로운 notch라는 인자를 지정할 수 있다. 이 값을 지정하면 중앙값에 대한 신뢰 구간이 오목하게 그려진다. 따라서 2개의 상자 그림을 나란히 그렸을 때 만약 두 상자 그림의 notch가 겹친다면 두 상자 그림의 중앙값이 다르지 않다고 볼 수 있다. 만약 겹치지 않는다면 두 상자 그림의 중앙값이 유의하게 다르다고 본다.

iris의 setosa 종과 versicolor 종의 Sepal.Width에 대한 상자 그림을 그린 다음, 이 두 종의 중앙값이 다른지 비교해보자.

> sv <- subset(iris, Species=="setosa" | Species=="versicolor")
> sv$Species <- factor(sv$Species)
> boxplot(Sepal.Width ~ Species, data=sv, notch=TRUE)

위 코드는 먼저 iris에서 Species가 setosa 또는 versicolor인 행을 선택했다. 이때 사용하는 OR 연산자는 벡터 연산이므로, ||가 아니라 |임에 유의하자.

코드의 두 번째 줄에서는 sv$Species를 다시 한 번 팩터로 변환했다. 이미 팩터인데 어째서 다시 팩터로 변환할까? 그 이유는 subset이 비록 두 개의 Species만 선택하는 역할은 하지만, Species 변수 자체를 바꾸지는 않기 때문이다. sv$Species는 subset( ) 후에도 여전히 레벨이 setosa, versicolor, virginica다. 따라서 실제 존재하는 레벨만 남기고 지우기 위해 다시 한 번 팩터로 변환을 해주었다. 그 결과 그림 6-31의 가로축에는 setosa와 versicolor만 나열되어 있다. 만약 남아 있는 virginica를 없애주지 않으면 텅 빈 virginica 컬럼이 추가로 보이게 된다.

마지막으로 세 번째 줄에서는 Sepal.Width의 상자 그림을 Species마다 그리기 위해 Sepal.Width ~ Species를 지정했다.

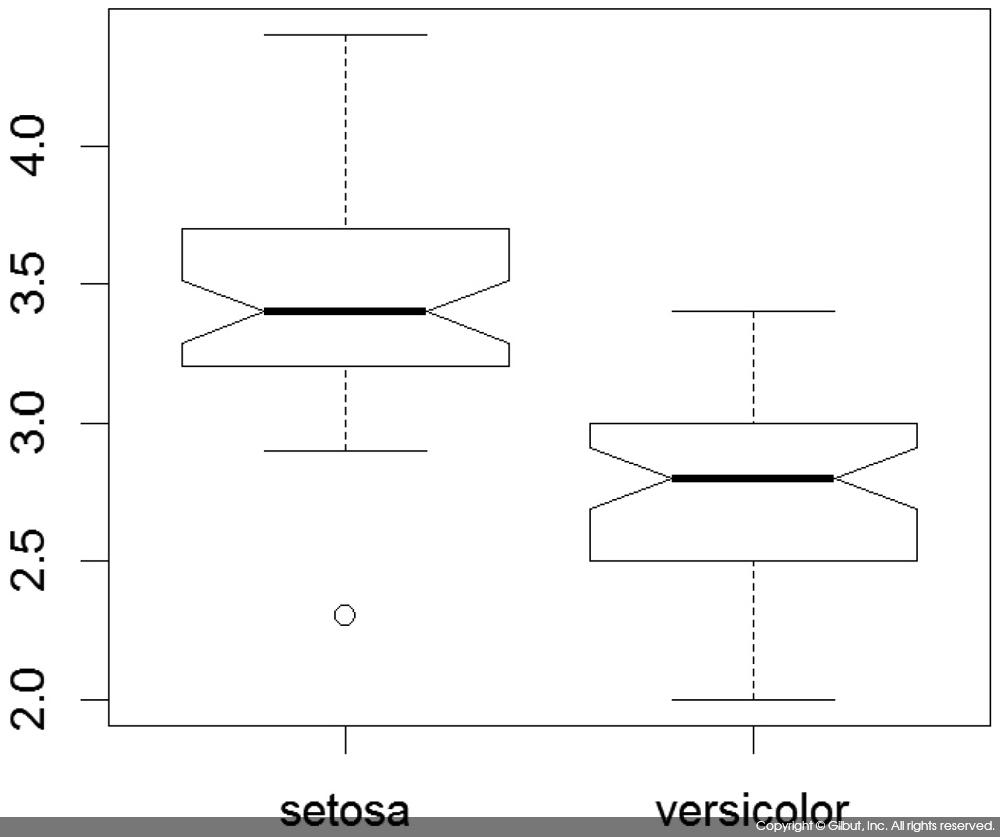
그림을 보면 setosa 종의 Sepal.Width가 전반적으로 versicolor 종의 Sepal.Width보다 큼을 알 수 있다.

이번에는 두 상자 그림에서 notch를 살펴보자. 그림을 보면 이전의 상자 그림과 달리 상자의 가운데 부분이 오목하게 들어가 있음을 볼 수 있다. 이 영역이 각각 setosa와 versicolor의 중앙값에 대한 일종의 신뢰 구간이다. setosa와 versicolor의 notch가 겹치지 않으므로 이 두 그룹의 중앙값은 서로 다르다고 결론을 내릴 수 있다.