히스토그램(hist)

데이터의 분포를 알아보는 데 유용한 또 다른 그래프는 히스토그램이다. 히스토그램은 값의 범위마다 빈도를 표시한 그래프다.

hist(
  x,  # 히스토그램을 그릴 값의 벡터
  # breaks는 히스토그램을 그리기 위해 데이터를 어떻게 나눌지를 지정하는 데 사용한다.
  # 기본값은 Sturge로, n일 때 막대의 너비를 ⌈log2(n)+1⌉로 정한다.
  # breaks에 데이터를 나눌 구분 값들을 저장한 벡터,
  # 데이터를 나눌 구분 값들을 계산하는 함수 등을 대신 지정할 수 있다.
  breaks="Struge",
  # freq가 지정되지 않거나 이 값이 TRUE면 데이터 빈도수에 히스토그램이 그려진다.
  # FALSE면 데이터의 확률 밀도를 그린다.
  freq=NULL,
  ...
)

다음은 iris$Sepal.Width에 대한 히스토그램을 그리는 예다.

> hist(iris$Sepal.Width)

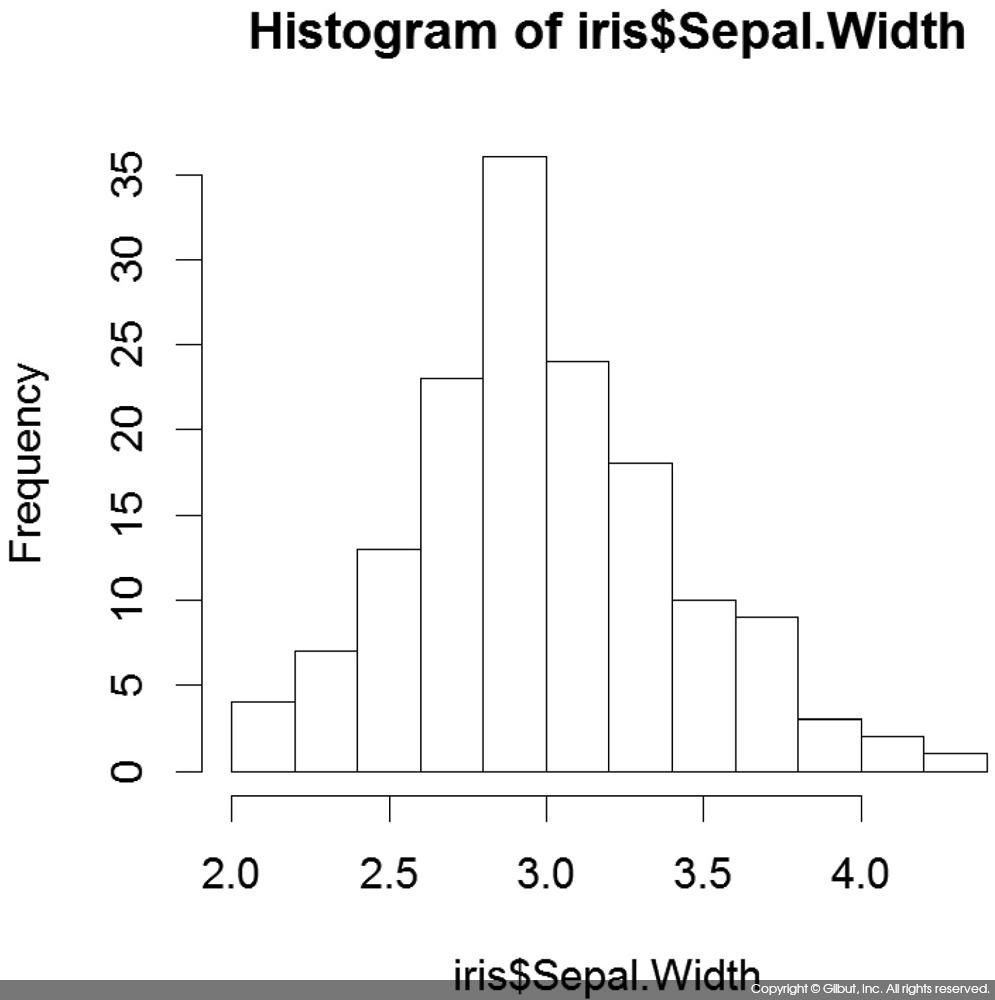
hist( )의 주요 파라미터 중 하나는 freq다. freq의 기본값은 NULL이며, 값을 지정하지 않으면 히스토그램 막대가 각 구간별 데이터의 개수(즉, 빈도)로 그려진다. 만약 이 값이 FALSE면 다음 코드에서 보다시피 각 구간의 확률 밀도11 가 그려진다. 확률 밀도므로 막대 너비의 합이 1이 된다.

> hist(iris$Sepal.Width, freq=FALSE)

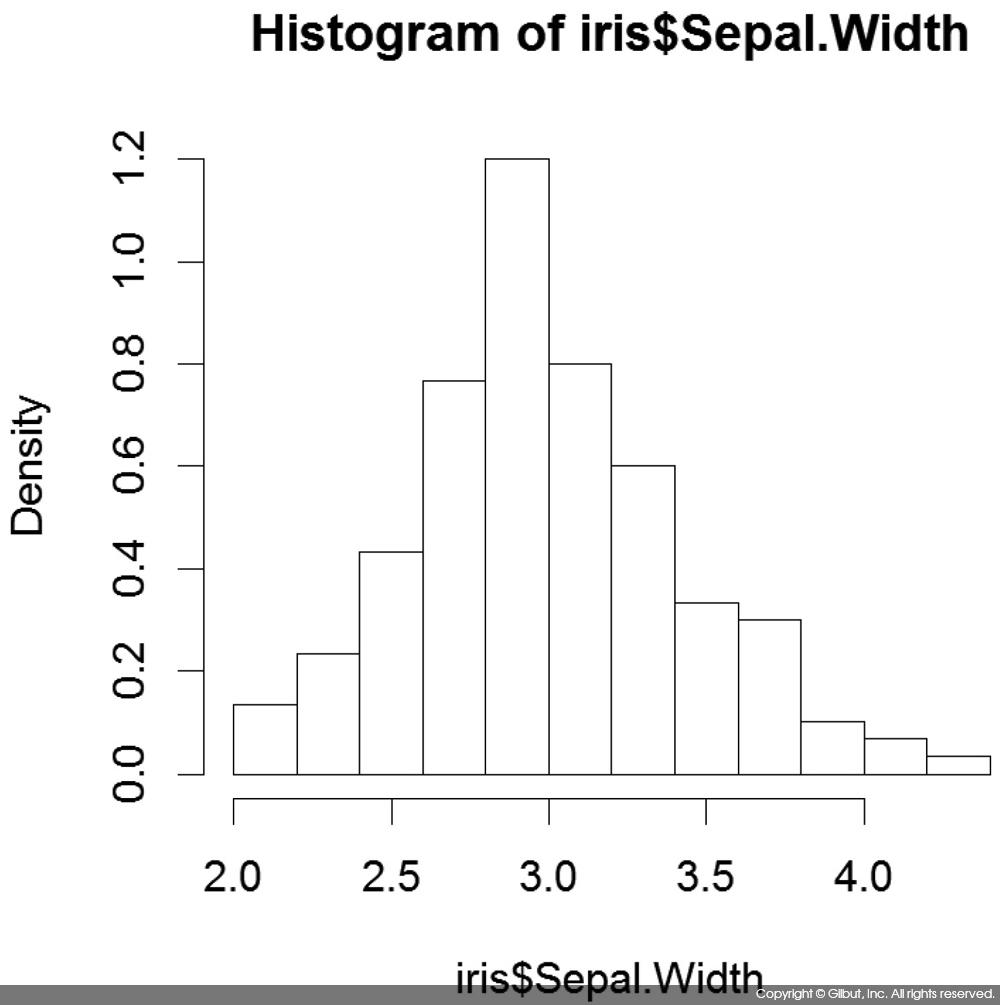
히스토그램을 그리면서 계산된 다양한 통계 값은 hist( )의 반환 값에 리스트로 저장되어 있다. 예를 들어, 다음 코드처럼 hist( )의 반환 값을 사용해 density 값의 합이 1임을 확인해볼 수 있다.

> (x <- hist(iris$Sepal.Width, freq=FALSE))
$breaks
[1] 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4

$counts
[1] 4 7 13 23 36 24 18 10 9 3 2 1

$density
[1] 0.13333333 0.23333333 0.43333333 0.76666667 1.20000000 0.80000000 0.60000000 0.33333333 0.30000000
[10] 0.10000000 0.06666667 0.03333333

$mids
[1] 2.1 2.3 2.5 2.7 2.9 3.1 3.3 3.5 3.7 3.9 4.1 4.3

$xname
[1] "iris$Sepal.Width"

$equidist
[1] TRUE

attr(,"class")
[1] "histogram"

> sum(x$density) * 0.2  # x$breaks를 보면 막대의 너비가 0.2임을 알 수 있다.
[1] 1

11 각 구간에 얼마만큼의 데이터가 속해 있는지를 확률로 나타낸 값이다.