outer( )를 사용해 X 축 그리드 seq(-3, 3, .1), Y 축 그리드 seq(-3, 3, .1)에 대해 이변량 정규 분포bivariate normal distribution13를 그려보자. persp( )에 넘길 Z 인자는 각 X, Y 그리드 점에 대해 확률 밀도인데, 다변량 정규 분포multivariate normal distribution의 확률 밀도는 mtvnorm 패키지의 dmvnorm( )을 사용해 계산한다. 다음은 x=0, y=0에 대해 x, y의 평균이 각각 0이고, 공분산 행렬covariance matrix이 2×2 크기의 단위행렬Identity Matrix일 때 확률 밀도를 구하는 예다.

> install.packages("mtvnorm")
> library(mvtnorm)
> dmvnorm(c(0, 0), rep(0, 2), diag(2))
[1] 0.1591549

다음 코드는 seq(-3, 3, .1)의 X, Y 축 그리드 조합에 대해 Z 축 값을 구한다. dmvnorm( )에서 평균의 기본값은 영행렬zero matrix이고, 공분산 행렬의 기본값은 단위행렬이다.

> x <- seq(-3, 3, .1)
> y <- x
> outer(x, y, function(x, y) { dmvnorm(cbind(x, y)) })

이제 모든 준비가 끝났다. 지금까지 살펴본 내용을 종합해 투시도를 그리는 코드는 다음과 같다.

> x <- seq(-3, 3, .1)
> y <- x
> f <- function(x, y) { dmvnorm(cbind(x, y)) }
> persp(x, y, outer(x, y, f), theta=30, phi=30)

코드에서 theta와 phi는 그림의 기울어진 각도를 지정하는 인자다. 이 두 인자에 지정할 값은 여러 값을 넣어 그림을 그려보면서 적절하게 정하면 된다. 결과는 다음과 같다.

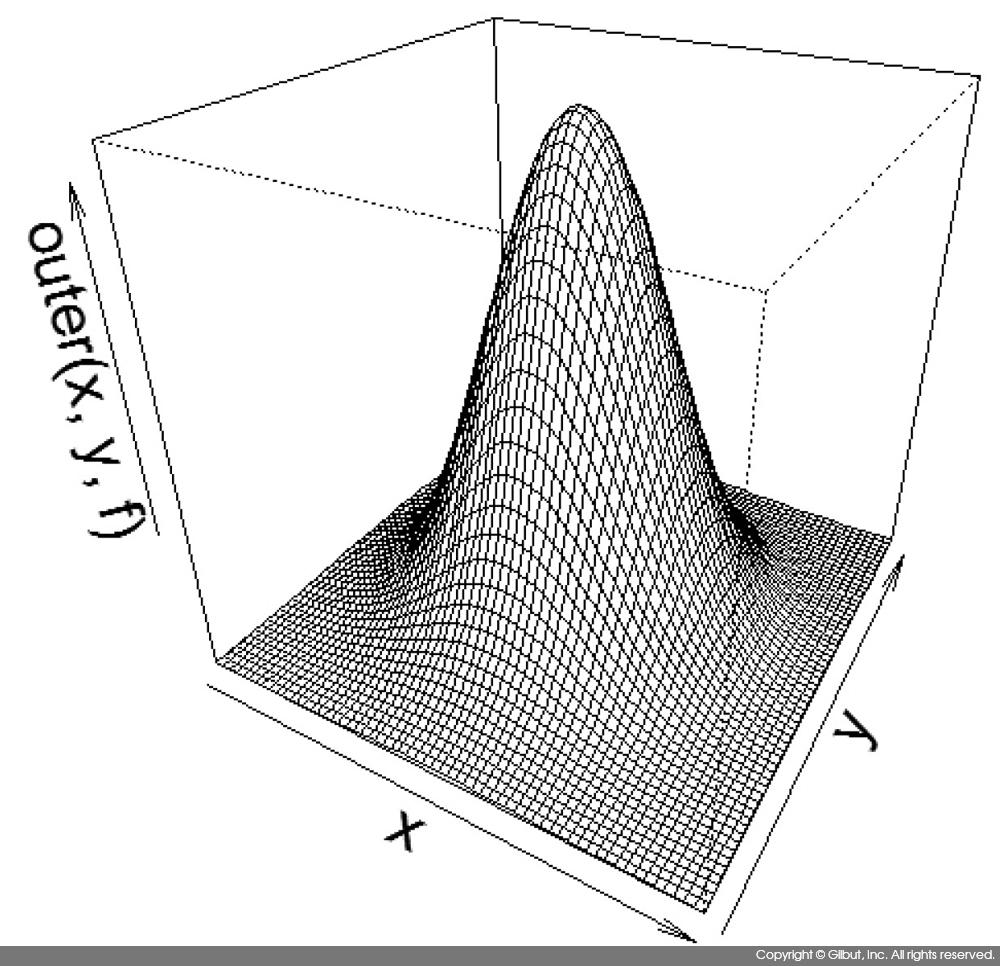
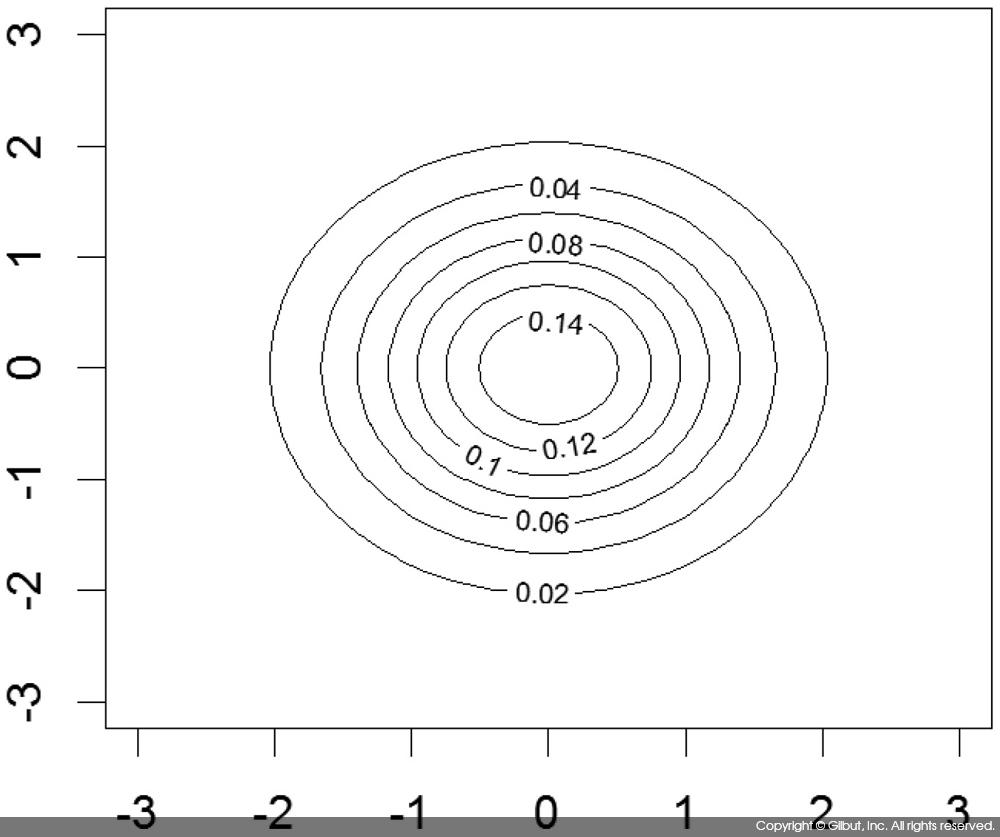
등고선 그래프는 투시도와 유사하지만 투시한 3차원 그림 대신 값이 같은 곳들을 선으로 연결한 등고선을 이용해 데이터를 표시한다. 등고선 그래프는 contour( )를 사용해 그린다. 다음은 이변량 정규 분포에 대한 등고선 그래프를 그리는 예다.

> contour(x, y, outer(x, y, f))

---

13 변수 2개의 분포가 정규 분포를 이루는 경우라고 생각하면 된다.