R을 이용한 데이터 처리 & 분석 실무: 난수 생성 및 분포 함수

확률 밀도 함수Probability Density Function 또는 확률 질량 함수Probability Mass Function는 d 뒤에 분포명을 적는다. 예를 들어, 정규 분포의 경우 dnorm( )을 사용한다.

분포 함수Distribution Function1 는 p 뒤에 분표명을 적은 형태다. 예를 들어, 정규 분포의 분포 함수는 pnorm( )이다.

분위수Quantile는 q 뒤에 분포명을 적으며, 정규 분포의 경우 qnorm( )으로 구한다. qnorm( )이 pnorm( )의 역함수에 해당하는데, p와 q가 알파벳에서 연속된 문자임을 상기하면 기억하기 쉽다.

위 세 가지 함수와 난수 발생 함수를 표 7-2에 정리했다.

<Note> 분포 함수와 확률 밀도 함수, 확률 질량 함수[1]

실험에서 나타난 결과를 실수로 표현한 변수 X를 확률 변수라 한다. 예를 들어, 동전 두 개를 던졌을 때 앞면의 개수 X, 웹 페이지의 하이퍼링크가 클릭된 수 X, 강수량 X가 확률 변수의 예다.

분포 함수는 확률 변수의 누적 분포를 기술하는 함수로, 보통 대문자 F를 써서 F(x)로 표현한다. 누적 분포 함수 F(x)는 확률 변수 X가 x 이하의 값을 가질 확률을 뜻한다. 즉, F(x) = P(X ≤ x)다.

확률 밀도 함수는 연속형 데이터의 확률을 표현한다. 강수량, 키, 몸무게 등의 값이 연속형 데이터의 예다. 확률 밀도 함수는 f(x)처럼 소문자로 표시한다. 그러나 연속형 데이터의 경우 x를 하나의 정확한 값으로 정하기가 곤란하다. 예를 들어, f(93.23483724)와 f(93.23483725)의 비교는 무의미하다. 따라서 f(x)는 구간에 대해 정의하며, 함수를 특정 구간에 대해 적분한 값이 확률 변수 X가 그 구간에 속할 확률이 되는 함수다. 다시 말해 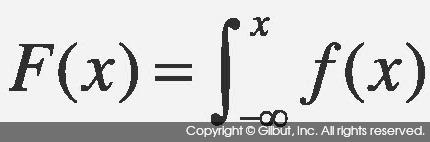다.

x가 이산형 값들만 가진다면 특정 x에 대한 확률을 계산할 수 있다. 예를 들어, 동전 한 개를 던졌을 때 앞면의 수를 X라 하면 P(X=1)은 앞면, 뒷면의 두 가지 가능성 중 하나에 해당하므로 1/2이다. 이러한 P(X=x)를 확률 질량 함수(Probability Mass Function)라고 하며, 흔히 보기 쉽게 p(x)로 적는다. 확률 질량 함수에서는 확률 밀도 함수와 달리 p(0), p(1)처럼 구간이 아닌 특정 값에 대한 확률을 이야기할 수 있다.

R에서 d로 시작하는 함수(예를 들면, dnorm 함수)는 f(x), p(x)를 계산하며, q로 시작하는 함수는 F(x)를 계산한다.

그림 7-2에 확률 밀도 함수와 분포 함수의 개념도를 보였다. 확률 밀도 함수의 그림이 주어졌을 때 f(X)는 x 값에 대한 확률 밀도 함수의 값 자체가 되고, F(x)는 X ≤ x인 모든 X에 대한 f(x)의 적분 값(즉, 확률 밀도 함수 영역의 넓이)이 된다.

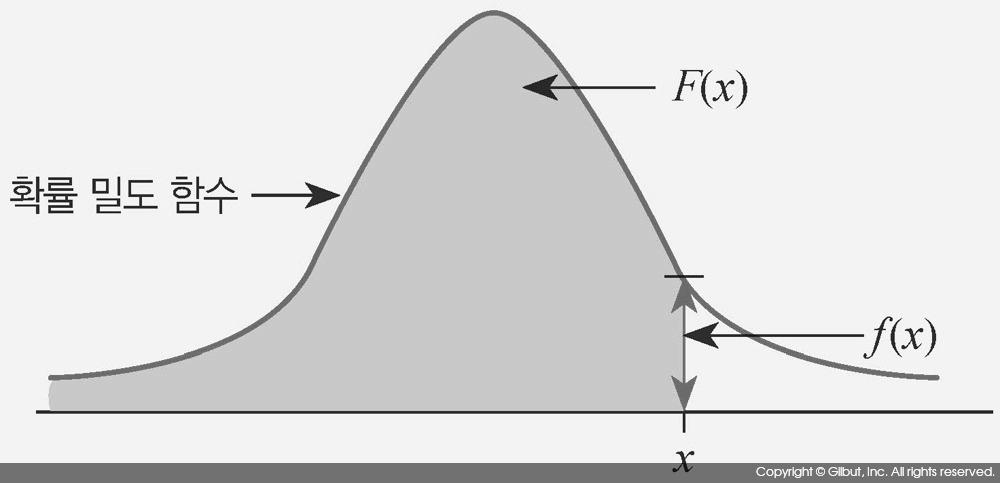
그림 7-2 확률 밀도 함수와 분포 함수의 개념 — ▼ **그림 7-2** 확률 밀도 함수와 분포 함수의 개념

<Note> 분포 함수와 분위수 함수의 관계

분포 함수 F(x)는 확률 밀도 함수 f(x)가 주어졌을 때

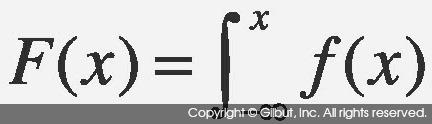로 정의된다. 즉, X가 x 이하의 값을 가질 확률을 뜻한다. 따라서 F(p) = q라면 X가 p보다 작은 비율이 q임을 뜻한다. 분위수 함수는 q를 주었을 때 F(p) = q인 p를 찾는다. 따라서 분포 함수의 역함수 F^-1( )로 이해하면 된다.

▼ 표 7-2 확률 분포 및 관련 함수

확률 분포	난수	확률 밀도 함수	분포 함수	분위수 함수
이항 분포	rbinom	dbinom	pbinom	qbinom
F 분포	rf	df	pf	qf
기하 분포	rgeom	dgeom	pgeom	qgeom
초기하 분포	rhyper	dhyper	phyper	qhyper
음 이항 분포	rnbinom	dnbinom	pnbinom	qnbinom
정규 분포	rnorm	dnorm	pnorm	qnorm
포아송 분포	rpois	dpois	pposi	qpois
t 분포	rt	dt	pt	qt
연속 균등 분포	runif	dunif	punif	qunif

이 함수들을 실제 코드로 연습해보자. 포아송 분포의 확률 질량 함수Probability Mass Function는 다음과 같다.

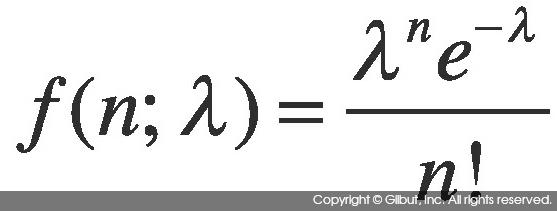
λ=1일 때 f(3; 1)을 구해보자.

> dpois(3, 1)
[1] 0.06131324
> (1^3 * exp(-1)) / (factorial(3))
[1] 0.06131324

실행 결과 dpois( )에서 구한 값과 수식으로 구한 값이 일치했다.

다음으로 N(0, 1)의 정규 분포에서 누적 분포 F(0) 그리고 50%에 대한 분위 수 F^-1(0.5)를 구해보자.

> pnorm(0)
[1] 0.5
> qnorm(0.5)
[1] 0

<Note> 정규 분포(Normal Distribution)의 파라미터

정규 분포는 평균(μ)과 분산(σ²)의 두 개 파라미터를 가지며 N(μ, σ²)로 표현한다.

1 누적 분포 함수(CDF, Cumulative Distribution Function)라고도 한다.

신간 소식 구독하기

뉴스레터에 가입하시고 이메일로 신간 소식을 받아 보세요.