독립성 검정
분할표의 행에 나열된 변수와 열에 나열된 변수가 독립이라고 가정하자. 만약 분할표에서 행과 열이 독립이라면 (i, j) 셀의 확률 P(i, j)에 대해 다음 식이 성립한다.
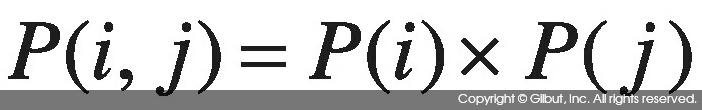
예를 들어, 다음 분할표를 생각해보자.
|
변수 A - True |
변수 A - False |
총계 |
|
|
변수 B - True |
30 |
70 |
100 |
|
변수 B - False |
50 |
40 |
90 |
|
총계 |
80 |
110 |
190 |
표에서 변수 A가 True일 확률은 80/190, 변수 A가 False일 확률은 70/190이다. 마찬가지로 변수 B가 True일 확률은 100/190, 변수 B가 False일 확률은 90/190이다. 따라서 만약 A와 B가 독립이라면 변수 A가 True이고, 변수 B가 True일 확률은 (80/190) * (100/190)이라고 할 수 있다. 독립성 검정Independence Test은 실제로 이와 같은 가정이 성립하는지 알아보는 것을 목표로 한다.
확률 이론에서 독립이란 두 사건이 서로 영향을 주고받지 않는 경우를 뜻한다. 반대로 독립이 아닌 경우는 한 사건이 다른 사건에 영향을 주는 경우를 뜻한다.
독립의 예로 동전을 두 번 던져 각각 앞면이 나왔는지 뒷면이 나왔는지를 기록하는 경우를 생각해보자. 처음 동전을 던졌을 때 앞면이 나오면 두 번째 동전을 던졌을 때 다시 앞면이 나올 확률이 높아질까? 그렇지 않다. 그렇다고 뒷면이 나올 확률이 높아지는 것도 아니다. 동전을 처음 던졌을 때 앞면이 나오든 뒷면이 나오든, 두 번째 던진 동전이 앞면이 나올지 뒷면이 나올지에는 영향이 없다. 즉, 동전 던지기에서 첫 번째 동전이 어느 면이 나오는지의 확률 분포와 두 번째 동전이 어느 면이 나오는지의 확률 분포는 서로 독립이다. 따라서 다음이 성립한다.
P(첫 번째 동전이 앞면, 두 번째 동전이 앞면) = P(첫 번째 동전이 앞면 ) × P(두 번째 동전이 앞면)7
이를 좀 더 일반화해서 표현해보자. 두 변수 A, B가 있을 때 A, B가 독립이면 P(A, B) = P(A) × P(B)가 성립한다.
반대로 독립이 아닌 예로는 항아리에서 구슬을 꺼내는 경우를 생각할 수 있다. 항아리에 빨간색 공이 5개, 파란색 공이 3개 있다고 가정하자. 그리고 이 항아리에서 두 개의 공을 하나씩 차례로 꺼내보자. 처음 꺼낸 공이 빨간색 공이면 다음 공이 파란색 공일 확률이 높아질까? 그렇다. 처음 공을 꺼낼 때 그 공이 파란색 공일 확률은 3/8이었지만, 빨간색 공을 하나 빼고 나면 파란색 공일 확률은 3/7이 된다. 즉, 처음 꺼낸 공이 어떤 색인지에 따라 다음 공이 어떤 색일지의 확률이 달라진다.
변수 간의 독립성 검정에는 카이 제곱 검정Chi-Squared Test을 사용하며, 이때 사용되는 통계량은 다음과 같다.
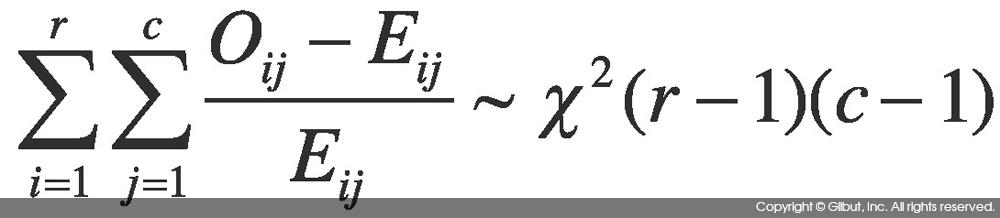
위 식에서 r은 행의 수, c는 열의 수를 의미한다. Oij는 분할표의 (i, j) 셀에 기록되어 있는 값이며, 분할표를 보면 바로 알 수 있는 값이다. Eij는 분할표의 두 변수가 독립일 때 (i, j) 셀에 대한 기댓값이다. 식 7-1에 의해 전체 데이터의 수가 n이라 할 때 Eij = n×P(i, j) = n×P(i)×P(j)다.
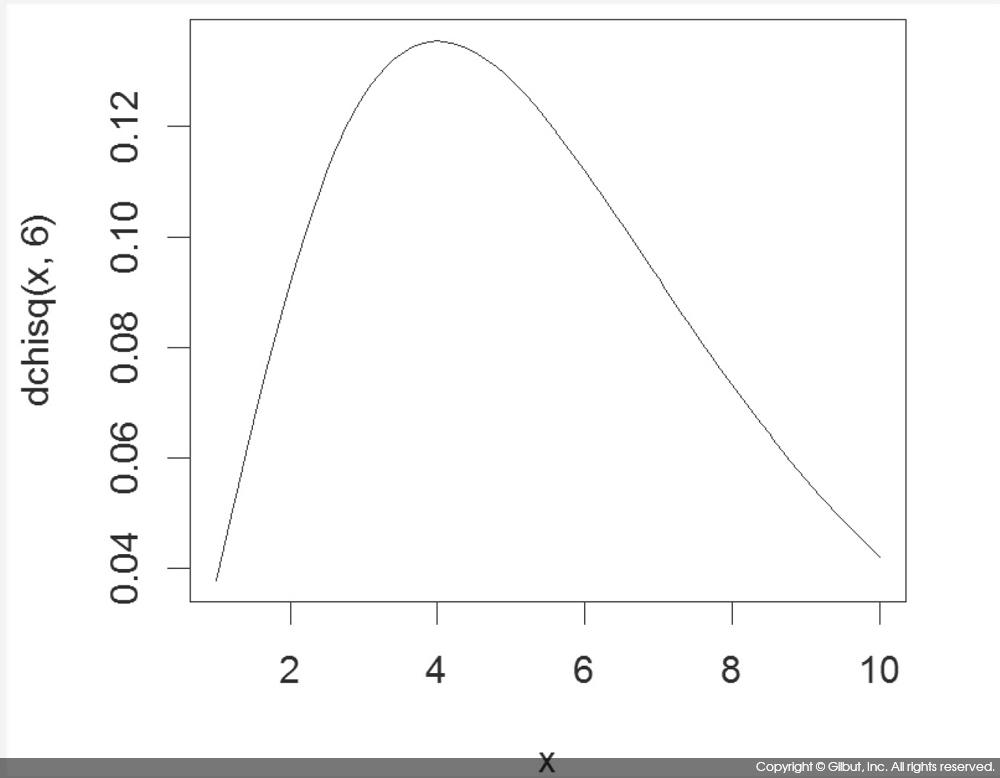
통계학에서 ~ 기호는 ~ 좌측에 있는 확률 변수가 ~ 우측에 있는 확률 분포를 따름을 의미한다. 따라서 χ2(r-1)(c-1)은 ~ 좌측의 식이 카이 제곱 분포를 따른다는 의미다. 카이 제곱 분포는 자유도(degree of freedom)라는 하나의 파라미터를 가지며, 이 파라미터에 따라 분포의 모양이 달라진다. 예를 들어, 분할표가 4행 3열이라면 (r-1)(c-1) = (4-1)(3-1) = 3×2 = 6이므로 χ2(6) 분포를 따른다는 의미다. 이때 6은 카이 제곱 분포의 자유도를 뜻한다. 그림 7-3에 χ2(6)을 보였다. 그림에서 x 축은 통계량
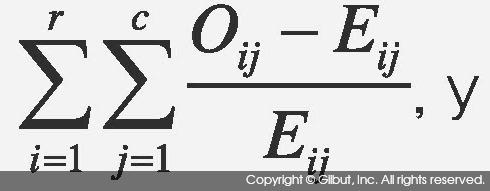, y 축은 해당 통계량을 가질 확률이다.
> x <- seq(1, 10, .1) > plot(x, dchisq(x, 6), type="l")
7 P(A, B)는 A와 B가 모두 일어난 경우를 뜻한다.