다음은 정규 분포를 따르는 두 난수 데이터 간에 분포가 동일한지를 살펴본 예다.

> ks.test(rnorm(100), rnorm(100))

   Two-sample Kolmogorov-Smirnov test

data: rnorm(100) and rnorm(100)
D = 0.1, p-value = 0.6994
alternative hypothesis: two-sided

p-value > 0.05이므로 두 난수가 같은 분포라는 귀무가설을 기각할 수 없다. 다음은 정규 분포와 균등 분포Uniform Distribution 간의 비교를 해보자.

<Note> 균등 분포

---

균등 분포는 주어진 구간의 값이 관찰될 확률이 일정한 확률 분포로, U(a, b)로 표현한다. 예를 들어, [0, 1] 구간에서 값이 관찰될 확률이 동일한 확률 분포는 U(0, 1)로 표현한다. 확률 밀도 함수는 다음과 같다.

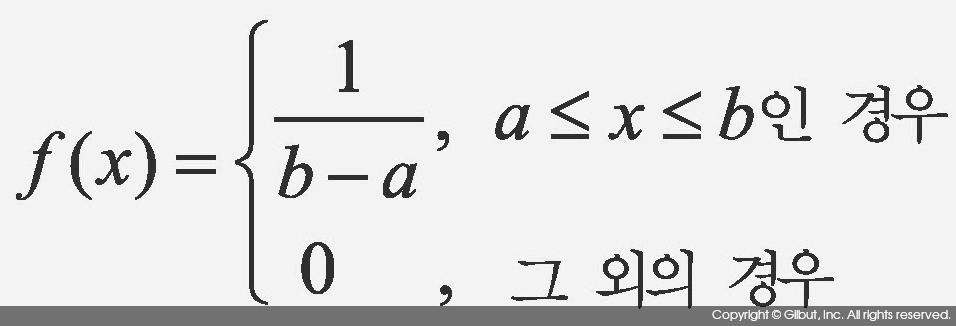
> ks.test(rnorm(100), runif(100))
   
   Two-sample Kolmogorov-Smirnov test

data: rnorm(100) and runif(100)
D = 0.56, p-value = 4.807e-14
alternative hypothesis: two-sided

p-value가 0.05보다 작아 서로 다른 분포로 판단되었다.

다음은 K-S 검정을 사용해 데이터가 평균 0, 분산 1인 정규 분포로부터 뽑은 표본인지 확인하는 예다.

> ks.test(rnorm(1000), "pnorm", 0, 1)

   One-sample Kolmogorov-Smirnov test

data: rnorm(1000)
D = 0.0399, p-value = 0.08342
alternative hypothesis: two-sided

귀무가설을 기각할 수 없어, 주어진 rnorm(100)은 평균 0, 분산 1인 정규 분포로부터의 표본이라고 결론을 내린다.