Q-Q도

Q-Q도Q-Q Plot는 데이터가 특정 분포를 따르는지를 시각적으로 검토하는 방법이다. Q는 분위수Quantile의 약어로 Q-Q도는 비교하고자 하는 분포의 분위수끼리 좌표 평면에 표시하여 그린 그림이다.

분위수들을 차트에 그리고 나면 데이터의 분위수와 비교하고자 하는 분포의 분위수 간에 직선 관계가 보이는지 확인한다. 예를 들어, X가 정규 분포를 따르는지 살펴보고 싶다고 가정하자. X ~ N(μ, α²)이라면 다음 관계가 성립한다.

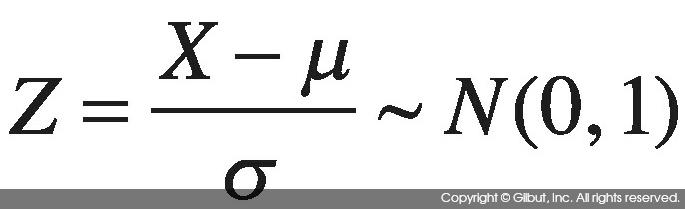
즉, 정규 분포를 따르는 확률 변수는 정규화된 뒤에 평균이 0, 분산이 1인 정규 분포를 따른다. X를 Z로 표현하면 다음과 같다.

따라서 X가 정규 분포를 따를 때 (X, Z)를 좌표 평면에 표시한다면 식 7-3에 보인 직선이 나타나야 한다. Q-Q도는 이와 같은 직선 관계가 실제로 성립하는지 시각적으로 보여주는 도구다.

(X, Z)에서 X는 주어진 데이터므로 이미 알고 있는 값이다. 따라서 X에 대응하는 Z만 찾으면 된다. 이때 분위수가 사용된다. X가 몇 % 분위수인지를 안다면 N(0, 1)에서 해당 % 분위수를 찾아 Z로 하면 된다.

X 값들이 몇 % 분위수인지 찾아보자. X를 크기 순서로 정렬했을 때 관측값 x₁ < x₂ < … < x_n이 된다고 하고, 이 데이터들의 분포를 표현하는 분포 함수가 다음과 같다고 하자.[11]

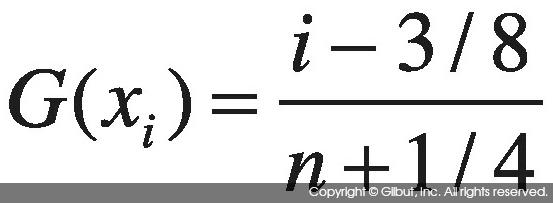
G(x_i)는 표본 데이터를 정렬했을 때 i번째 데이터가 몇 % 분위수인지 알려주는 역할을 한다. 예를 들어, 표본의 크기 n이 20이라면 G(x₁)=(1-3/8)/(20+¼)=0.03, G(x₂)=(2-3/8)/(20+2/4), …이 된다. 따라서 x₁은 X가 따르는 분포의 3% 분위수, x₂는 7% 분위수 등이 된다.

X가 몇 % 분위수인지 알면 Z는 손쉽게 찾을 수 있다. Z가 표준 정규 분포를 따르므로 3% 분위수인 z₁, 7% 분위수인 z₂ 등은 Z의 누적 분포 함수가 Φ라 할 때 z₁=Φ^-1(0.03), z₂=Φ^-1(0.07)이다.

지금까지 설명한 내용을 정리하면 X가 정규 분포를 따른다는 가정 하에서 다음이 성립한다.[11]

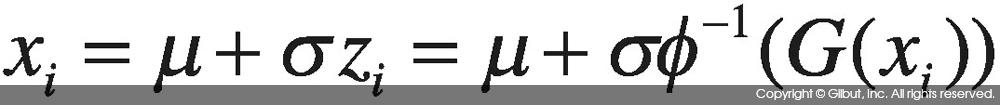
이제 X에 해당하는 Z를 찾았으니 (X, Z)를 그려볼 차례다. 이 목적으로는 qqnorm( ) 함수를 사용한다. qqline( )은 Q-Q도에서 데이터가 만족해야 하는 직선 관계를 그린다.

qqnorm(
  y  # 데이터 셋
)

qqplot(
  x,
  y
)

qqline(
  y,
  distribution=qnorm  # 이론적 분포에 대한 quantile 함수
)