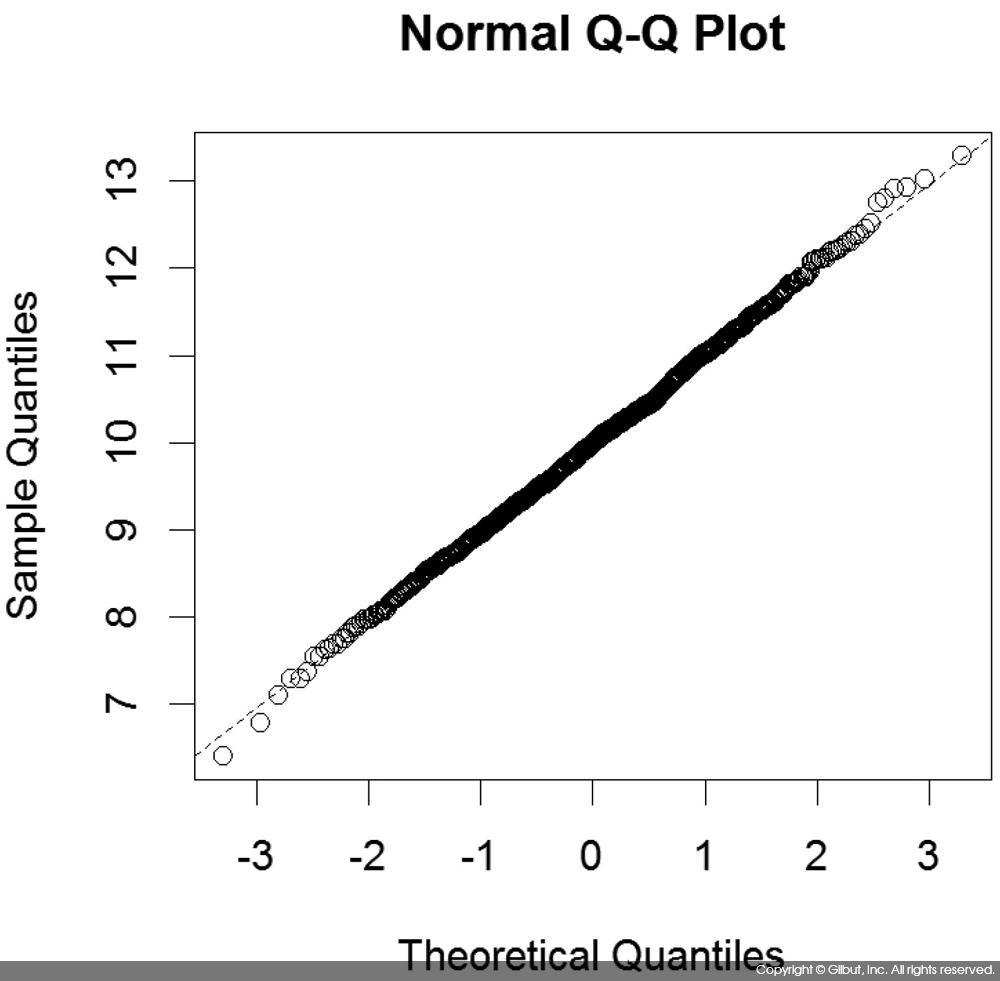
다음은 N(10, 1)의 정규 분포를 따르는 난수 1,000개를 구하고 Q-Q도를 그려 해당 숫자들이 정규 분포를 따르는지 확인해본 예다.

> x <- rnorm(1000, mean=10, sd=1)
> qqnorm(x)
> qqline(x, lty=2)

그림 7-8은 위 코드의 실행 결과로 그려진 Q-Q도다. 정규 분포에 대한 그림이므로 정규 확률 그림Normal Q-Q Plot이라고 한다. 그림에서 볼 수 있듯이 직선 관계가 잘 성립한다.

비교를 위해 균등 분포로부터 생성한 데이터로 정규 확률 그림을 그려보자. 결과를 보면 한눈에도 직선 관계가 성립하지 않음을 알 수 있다.

> x <- runif(1000)
> qqnorm(x)
> qqline(x, lwd=2)

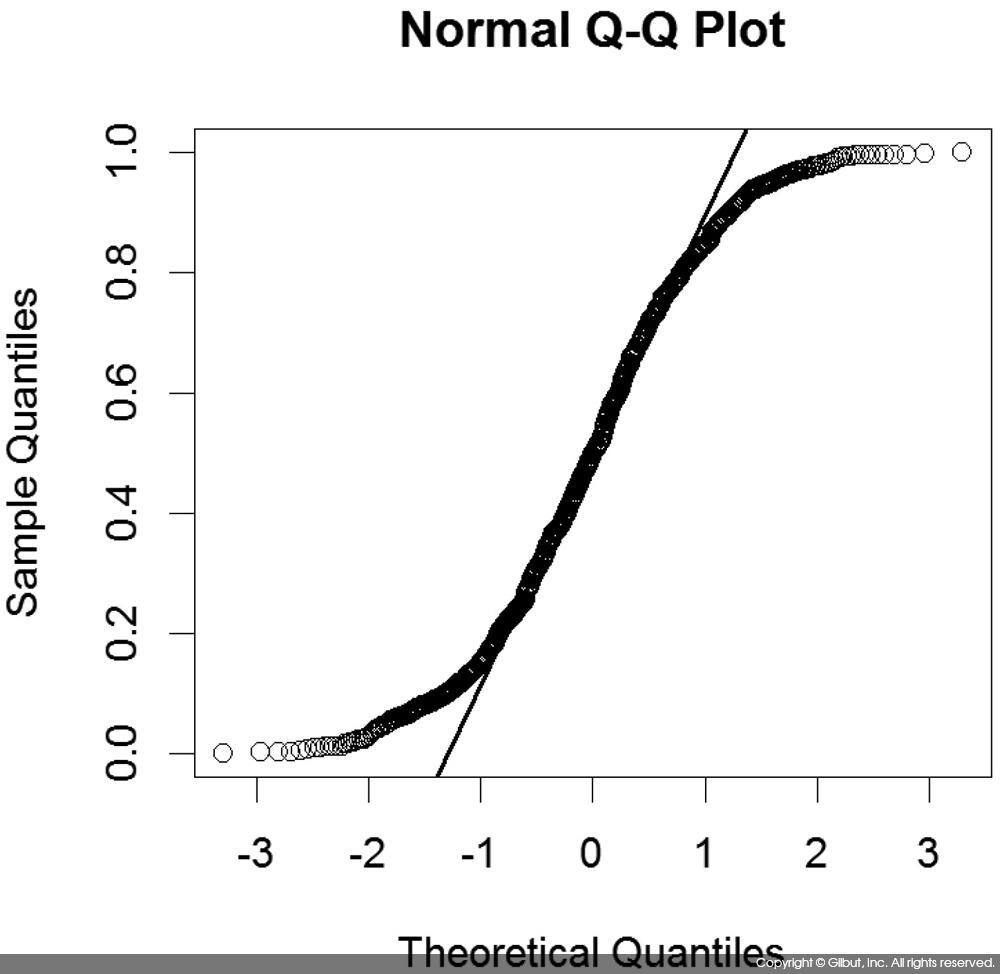
데이터의 정규성이 Q-Q도를 통해 항상 명확히 판단되는 것은 아니다. 직선 관계가 성립한다 할지라도 데이터의 출처 및 데이터가 정규성을 따를 이유에 대한 고민이 항상 필요하다.

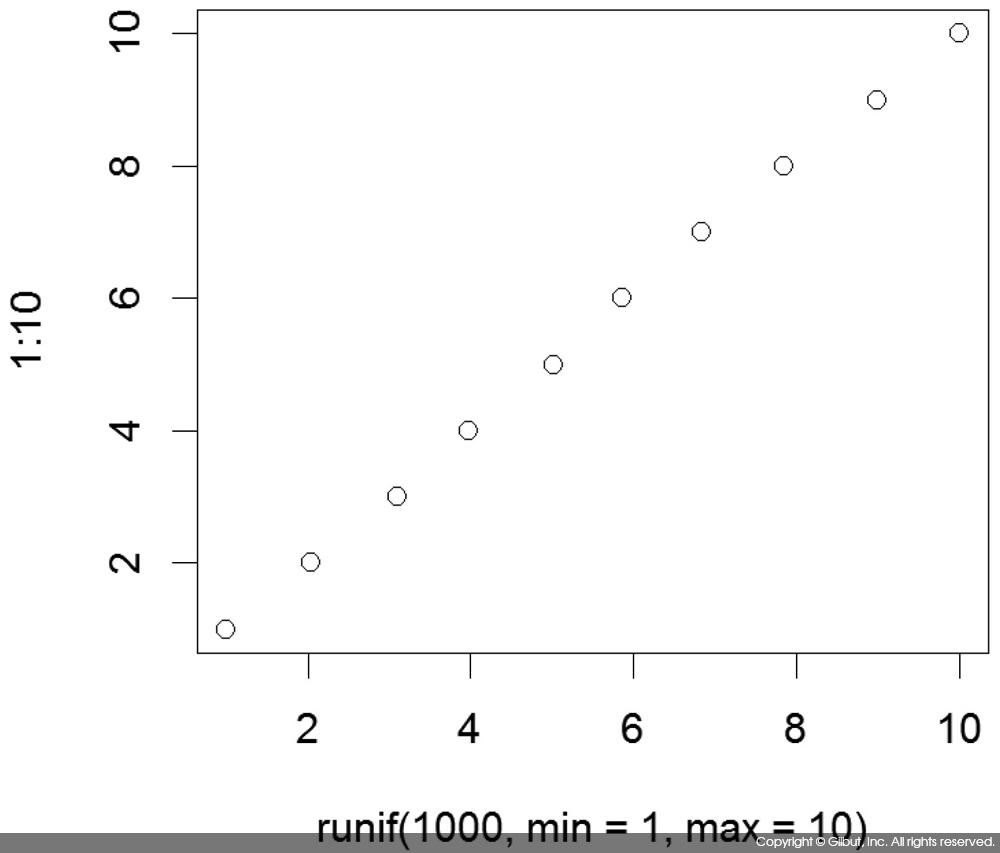
정규 확률 그림이 아닌 분포에 대해서는 qqplot( ) 함수를 사용한다. 다음은 c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)이 U(1, 10)의 균등 분포를 따르는지 확인하기 위해 Q-Q도를 그린 예다. 비교할 대상인 U(1, 10)은 runif( )로 데이터를 만들었다.

> qqplot(runif(1000, min=1, max=10), 1:10)

그림 7-10에 보인 것처럼 직선 관계가 잘 성립한다.