스피어만 상관 계수

스피어만 상관 계수Spearman’s Rank Correlation Coefficient[15]는 상관 계수를 계산할 두 데이터의 실제 값 대신 두 값의 순위rank를 사용해 상관 계수를 계산하는 방식이다. 피어슨 상관 계수와 마찬가지로 값의 범위는 [-1. 1]이며 1은 한쪽의 순위가 증가함에 따라 다른 쪽의 순위도 증가함을 뜻하고, -1은 한쪽의 순위가 증가할 때 다른 쪽의 순위는 감소함을 뜻한다. 0은 한쪽의 순위 증가가 다른 쪽의 순위와 연관이 없음을 뜻한다.

스피어만 상관 계수의 계산식은 피어슨 상관 계수와 유사해 이해하기 쉽고, 피어슨 상관 계수와 달리 비선형 관계의 연관성을 파악할 수 있다는 장점이 있다. 또한, 데이터에 순위만 매길 수 있다면 적용이 가능하므로 연속형Continuous 데이터에 적합한 피어슨 상관 계수와 달리 이산형Discrete 데이터, 순서형Ordinal 데이터에 적용이 가능하다. 예를 들어, 국어 점수와 영어 점수 간의 상관 계수는 피어슨 상관 계수로 계산할 수 있고, 국어 성적 석차와 영어 성적 석차의 상관 계수는 스피어만 상관 계수로 계산할 수 있다.

스피어만 상관 계수는 다음과 같이 정의한다.[16]

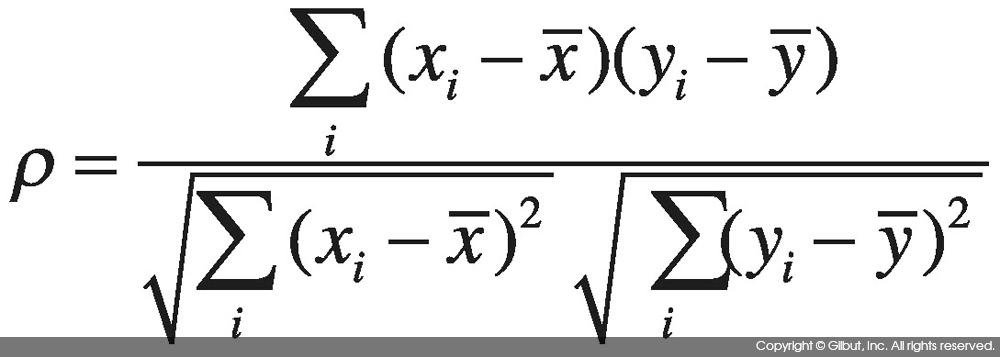
위 식에서 x_i는 변수 X에서 i번째 데이터의 순위, y_i는 Y에서 i번째 데이터의 순위, , 는 각각 x_i, y_i의 평균을 뜻한다. 이 식을 피어슨 상관 계수와 비교해보면 모양이 상당히 유사함을 알 수 있다.

식 7-5는 d_i = x_i - y_i라 놓으면 다음과 같이 간단히 할 수 있다.

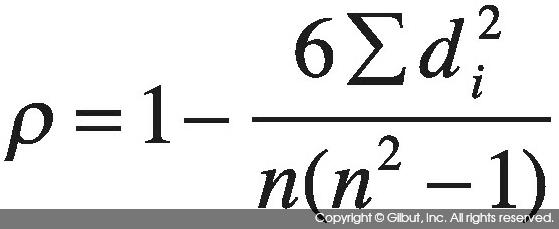
데이터가 주어졌을 때 순위 계산은 다음과 같이 한다. 예를 들어, 3, 4, 5, 3, 2, 1, 7, 5를 가정해보자. 이 데이터를 정렬하면 1, 2, 3, 3, 4, 5, 5, 7이 된다. 또, 각 값의 순위는 1, 2, 3.5, 3.5, 5, 6.5, 6.5, 8이 된다. 데이터에서 3, 3은 순위 3, 4에 해당하므로 이들의 평균인 3.5가 순위로 주어지고 5, 5는 순위가 6, 7위이므로 평균인 6.5가 순위로 주어진다. R 코드를 사용해 순위를 확인해보자.

> x <- c(3, 4, 5, 3, 2, 1, 7, 5)
> # rank() 함수를 사용하기 위해 sort()를 할 필요는 없다. 보기 편하게 하려고 정렬한 것일 뿐이다.
> rank(sort(x))
[1] 1.0 2.0 3.5 3.5 5.0 6.5 6.5 8.0

이처럼 비교할 데이터로부터 순위를 구한 다음 식 7-6을 적용하면 된다. R 코드에서는 스피어만 상관 계수 계산 시와 마찬가지로 cor( ) 함수를 사용한다. 다음은 가상의 순위가 저장된 행렬로부터 스피어만 상관 계수를 계산한 예다. 숫자가 양쪽에서 모두 증가하므로 스피어만 상관 계수는 1로 계산된다.

> (m <- matrix(c(1:10, (1:10)^2), ncol=2))
      [,1] [,2]
 [1,]    1    1
 [2,]    2    4
 [3,]    3    9
 [4,]    4   16
 [5,]    5   25
 [6,]    6   36
 [7,]    7   49
 [8,]    8   64
 [9,]    9   81
[10,]   10  100

> cor(m, method="spearman")
     [,1] [,2]
[1,]    1    1
[2,]    1    1

반면 같은 값을 피어슨 상관 계수에 넣으면 선형 관계를 따지게 되어 컬럼 1, 2 간의 상관 계수가 0.9745586으로 1보다 작게 나타난다.

> cor(m, method="pearson")
          [,1]      [,2]
[1,] 1.0000000 0.9745586
[2,] 0.9745586 1.0000000