일표본 평균

이 절에서는 하나의 모집단으로부터 표본을 추출하고 표본으로부터 모집단 평균의 신뢰 구간을 구하는 방법을 살펴본다.

이론적 배경

확률 변수 X₁, X₂, …, X_n이 서로 독립이고 정규 분포 N(μ, σ²)을 따른다고 하자. 즉, X_i는 N(μ, σ²)으로부터 구한 표본이며, 표본의 크기는 n이다. 표본의 평균이 X라 할 때 다음이 같이 평균이 0, 분산이 1인 정규 분포를 따르는 식을 구할 수 있다.

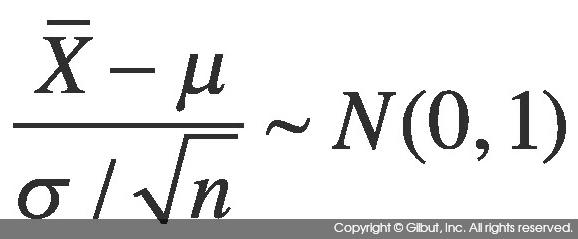
모집단의 분산 σ²은 보통 알려진 값이 아니므로 다음에 정의된 표본 분산을 사용한다.

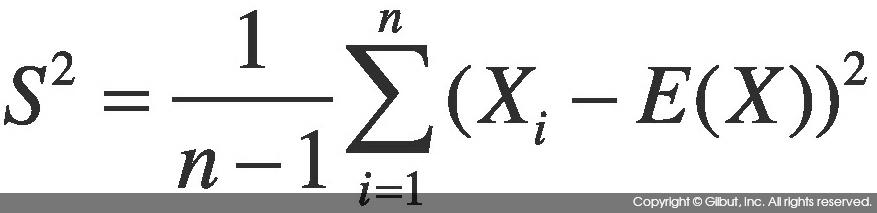
식 7-8에 σ² 대신 S²을 사용하면 자유도가 n - 1인 t 분포를 따르게 된다.

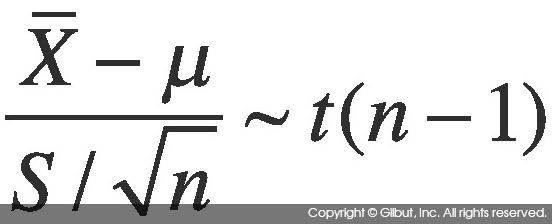
따라서 유의수준 α가 0.05일 때 모평균에 대한 95% 신뢰 수준의 신뢰 구간은 다음과 같다.

<Note> 모평균, 모분산, 표본 평균, 표본 분산

---

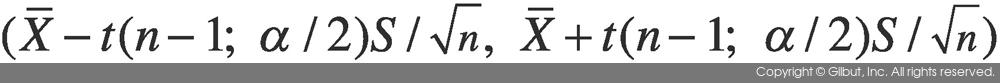
모평균은 모집단(연구 대상이 되는 전체)에서 구한 평균이다. 마찬가지로 모분산은 전체 데이터에 대한 분산을 뜻한다. 표본 평균은 모집단으로부터 추출한 표본의 평균이며, 표본 분산은 표본의 분산을 뜻한다. 모평균은 μ, 모분산은 σ^{2,/으로 표현한다. 표본 평균과 분산은 표본을 X₁, X₂, ..., X_n으로 표현할 때 각각 , S_X2으로 적는다.}

가설 검정 및 추정에서 하는 일은 표본의 평균과 분산으로부터 모집단의 평균과 분산을 알아내고자 하는 것이다.