독립 이표본 평균

이 절에서는 두 모집단에서 각각 표본을 추출한 뒤 표본으로부터 두 모집단의 평균이 같은지 알아보는 내용을 다룬다. 예를 들어, A 학교 학생의 평균 키와 B 학교 학생의 평균 키를 비교하기 위해 각 학교에서 100명씩 총 200명을 뽑아 키를 측정하여 두 학교 학생 키의 평균에 차이가 있는지 알아보는 경우를 생각해볼 수 있다.

이론적 배경

독립 이표본은 서로 독립인 두 개의 표본 집단이 있는 경우를 지칭한다. X₁, X₂, …, X_m이 N(μ₁, σ₁²)으로부터의 표본이고 Y₁, Y₂, …, Y_n이 N(μ₁, σ₂²)으로부터의 표본이라고 하자. X, Y는 독립이다.

그러면 표본의 평균 X, Y는 다음의 정규 분포를 따른다.

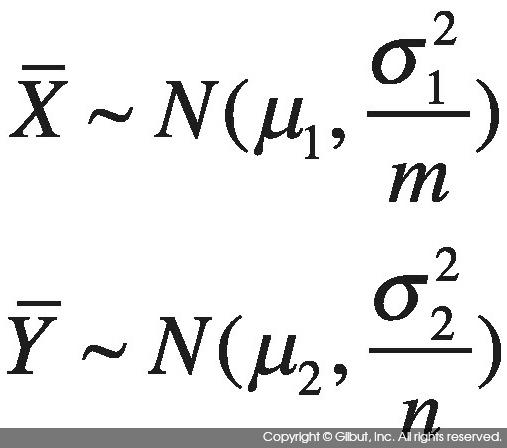
X와 Y가 독립이므로 다음이 성립한다.

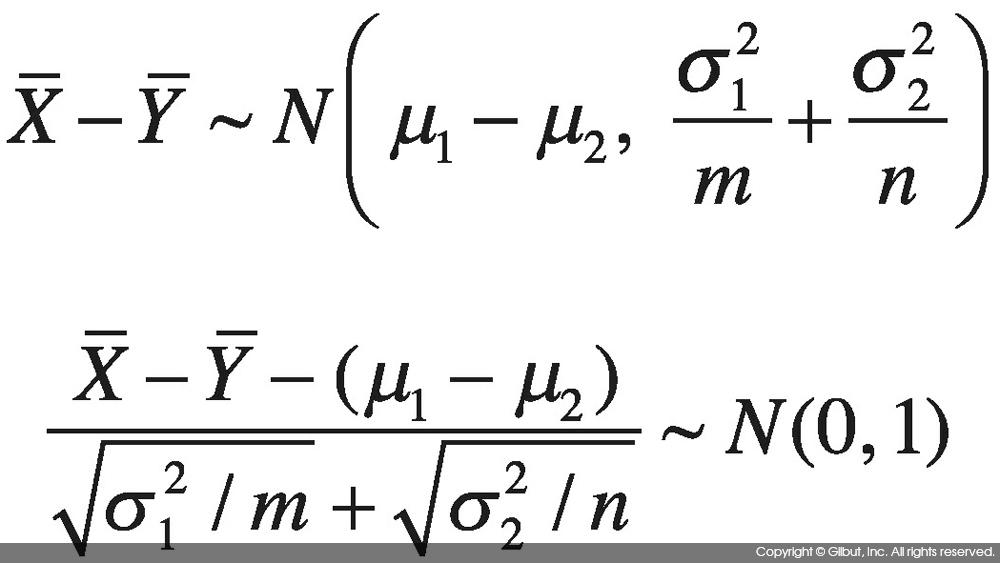
일표본 평균의 경우와 마찬가지로 σ₁², σ₂²은 모두 모집단의 분산이고, 이 값은 보통 사전에 알려지지 않은 값이다. 따라서 표본 분산을 대신 사용하게 된다. 표본 분산을 구할 때는 σ₁=σ₂인 경우와 σ₁≠σ₂를 나누어 풀이한다. 여기서는 모분산이 같은 경우(σ₁=σ₂)만 알아보도록 하자.

σ₁=σ₂인 경우9 합동 표본 분산Pooled Sample Variance S_p²을 구하여 σ₁, σ₂ 대신 사용한다. 합동 표본 분산은 두 집단의 표본 분산이 각각 S₁, S₂일 때 다음과 같다.

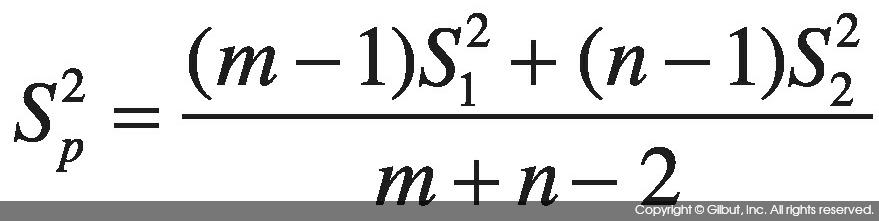
Sp를 식 7-10에 대입하면 다음과 같이 자유도가 m + n - 2인 t 분포를 따르게 된다.

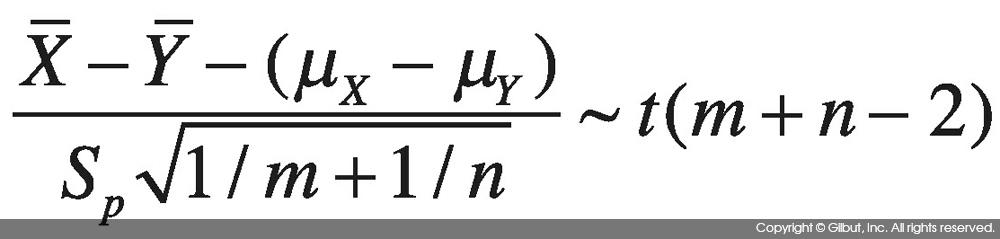
따라서 두 표본으로부터 구한 모평균 차이의 95% 신뢰 구간은 다음과 같다.

---

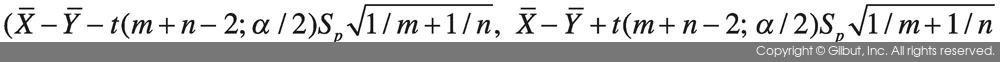
9 뒤에서 다룰 F-test를 사용해 실제로 분산의 차이가 있는지를 검정할 수 있다.