이표본 분산

이 절에서는 두 모집단으로부터의 표본으로부터 분산을 구해 두 모집단의 분산이 동일한지를 알아보는 방법에 대해 설명한다. 보통은 이표본 분산을 그 자체로 사용하기보다는 다른 통계 추정, 검정에서 이표본 분산의 결과를 사용하게 된다. 예를 들어, 독립 이표본 검정에서 두 모집단의 분산이 같으면 t.test( )의 인자로 var.equal=TRUE를, 다르면 var.equal=FALSE를 지정해야 한다고 설명한 바 있다.

이론적 배경

확률 변수 X, Y가 독립이며 X~N(μ₁, σ₁²), Y~N(μ₂, σ₂²)으로 각각 정규 분포를 따른다고 가정하자. m은 X에서의 표본 수, n은 Y에서의 표본 수다. 이때 표본 분산과 모분산의 비가 다음과 같이 F 분포를 따른다.

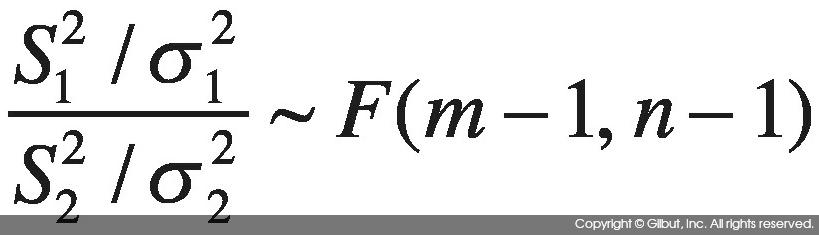
따라서 모분산 비에 대한 95% 신뢰 구간은 α=0.05라 할 때 다음과 같다.

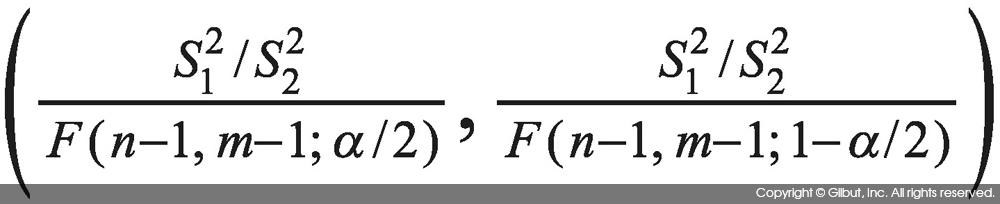
추정 및 검정의 예

분산의 비교에는 var.test( ) 함수를 사용한다.

var.test(
  x,        # 숫자 벡터
  y,        # 숫자 벡터
  ratio=1,  # 분산 비에 대한 가설
  alternative=c("two.sided", "less", "greater"),  # 대립가설. 기본값은 양측 검정(two.sided)
  ...
)

var.test(
  formula,  # lhs ~ rhs 형태로 쓰며 lhs는 검정에 사용할 값, rhs는 두 개의 그룹을 뜻하는 팩터
  data      # 포뮬러가 적용될 행렬 또는 데이터 프레임
)

iris의 Sepal.Width와 Sepal.Length가 같은지 var.test( )를 사용하여 검정해보자.

> with(iris, var.test(Sepal.Width, Sepal.Length))

   F test to compare two variances

data:  Sepal.Width and Sepal.Length
F = 0.2771, num df = 149, denom df = 149, p-value = 3.595e-14
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.2007129 0.3824528
sample estimates:
ratio of variances
         0.2770617

수행 결과 p-value가 매우 작게 나타났다. 따라서 모분산에 차이가 없다(ratio=1)는 귀무가설을 기각한다.