일표본 비율

모집단에서 표본을 추출하여 그 표본에서 계산한 비로부터 모집단의 비를 추정 및 가설 검정하는 내용에 대해 살펴보자. 일표본 비율의 예로는 국민 투표로 찬반 투표를 실시할 때 출구 조사를 들 수 있다. 투표자 중 임의의 표본(예를 들면, 1,000명의 유권자)에게 찬성과 반대 중 어느 쪽에 투표했는지를 물으면 찬성과 반대 중 어느 쪽의 비율이 크게 나타날지 추정할 수 있다.

이론적 배경

베르누이 시행Bernoulli Trial을 n회 수행하여 X번 성공했다고 하자.

이때 X는 성공 확률이 p인 베르누이 시행을 n회 수행했을 때 성공 횟수를 뜻하는 이항 분포Binomial Distribution를 따른다. 이를 다음과 같이 표현한다.

일표본 비율에서는 p를 구하는 것이 목적이다.

이항 분포 B(n, p)는 평균이 np, 분산이 np(1-p)며, n이 크면 정규 분포로 근사할 수 있다.

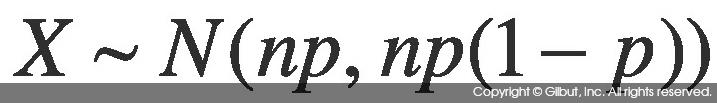
모비율에 대한 추정값 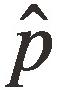는 X/n으로 계산할 수 있으므로 위 식의 양변을 n으로 나누면 다음과 같다.

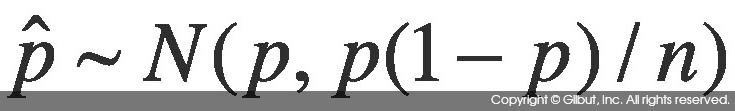
따라서 α=0.05라 할 때 모비율의 95% 신뢰 구간은 다음과 같다.

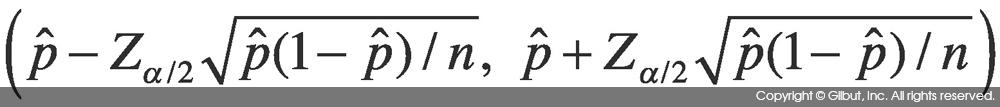
추정 및 검정의 예

비율에 대한 가설 검정 시 이항 분포의 정규 분포 근사를 사용할 경우 prop.test( )를 사용한다. 반면 이항 분포를 정규 분포로 근사하지 않고 그대로 사용해 계산하고 싶다면 binom.test( )를 사용한다(표 7-14 참고).

prop.test(
  x,         # 성공 횟수를 저장한 벡터 또는 성공과 실패 수를 저장한 1x2 또는 2x2 표(행렬)
  n,         # 전체 시행 수
  p = NULL,  # 비율
  alternative = c("two.sided", "less", "greater")  # 대립가설
)

동전을 100번 던졌더니 앞면이 42번 나왔다고 하자. 이때 동전의 앞면이 나오는 비율이 50%가 아니라고 할 수 있을까? prop.test( ) 함수로 확인할 수 있다.

> prop.test(42, 100)

   1-sample proportions test with continuity correction

data:  42 out of 100, null probability 0.5
X-squared = 2.25, df = 1, p-value = 0.1336
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.3233236 0.5228954
sample estimates:
   p
0.42

수행 결과 p-value > 0.05이므로 동전의 앞면이 나올 확률이 0.5라는 귀무가설을 기각할 수 없다. 이는 신뢰 구간 (0.32, 0.52)에 0.5가 포함되어 있는 것으로도 확인할 수 있다.

비율의 구간 추정 또는 검정 시 반드시 정규 분포 등으로 근사를 해야 하는 것은 아니다. binom.test( )를 사용하면 이항 분포로부터의 신뢰 구간을 직접 계산한다.

> binom.test(42, 100)

   Exact binomial test

data:  42 and 100
number of successes = 42, number of trials = 100, p-value = 0.1332
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.3219855 0.5228808
sample estimates:
probability of success
                  0.42

이항 분포를 통한 정확한 계산의 경우에도 동전의 앞면이 나올 확률이 0.5라는 귀무가설을 기각하지 못한다.