선형 회귀 결과 추출

lm( )으로 구한 모델의 세부 내용을 살펴보기 위한 함수들을 알아보자.

회귀 계수: coef(model)

다음은 선형 회귀 모델의 절편이 -17.579095, speed에 대한 기울기가 3.932409임을 보여준다.

> coef(m)
(Intercept)      speed
 -17.579095   3.932409

적합된 값: fitted(model)

cars 데이터의 각 speed 값에 대해 모델에 의해 예측된 dist 값은 fitted( )로 구할 수 있다. 이 값은 모델이 데이터에 적합fit된 결과이므로 적합된 값fitted value라고 부른다. 다음은 cars 데이터의 1~4번째 데이터에 대한 적합된 값들을 보여준다.

> fitted(m)[1:4]
        1         2         3         4
-1.849460 -1.849460  9.947766  9.947766

즉, 이 값은 -17.57095 + 3.932409 × cars$speed에 해당한다.

잔차: residuals(model)

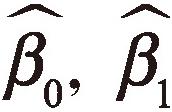식 8-1에서 ε_i는 오차error라고 불렀다. 이는 이론적인 값을 부르는 명칭이며, 실제로 선형 회귀 모델을 작성한 다음 모델로부터의 구한 예측값과 실제 값 사이의 차이는 잔차residual라고 부른다. 예측값은 로 표시하며 데이터로부터 구한 β₀, β₁의 추정값이 각각 이라 할 때 다. 잔차는 e_i로 표시하며 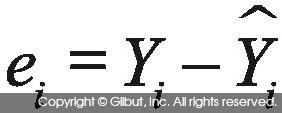다.

다음은 1~4번째 데이터에 대한 잔차를 구하는 예다.

> residuals(m)[1:4]
       1         2         3         4
3.849460 11.849460 -5.947766 12.052234

적합된 값과 잔차의 합은 실제 데이터 값과 같다. 다음은 cars에 적합된 값과 잔차의 합이 cars$dist와 같음을 보여주는 예다.

> fitted(m)[1:4] + residuals(m)[1:4]
1  2  3  4
2 10  4 22

> cars$dist[1:4]
[1]  2 10 4 22

회귀 계수의 신뢰 구간: confint(model)

단순 선형 회귀에서 절편과 speed의 기울기는 정규 분포를 따른다. 따라서 t 분포를 사용한 신뢰 구간을 confint(model)을 사용해 구할 수 있다.

> confint(m)
                 2.5 %    97.5 %
(Intercept) -31.167850 -3.990340
speed         3.096964  4.767853

잔차 제곱 합

잔차 제곱 합 은 다음과 같이 구한다.

> deviance(m)
[1] 11353.52

<Note> 최소 제곱법

---

선형 회귀의 회귀 계수 β₀, β₁, ..., β_p는 최소 제곱법(Method of Least Square)으로 추정한다. 최소 제곱법이란 제곱의 합이 최소가 되도록 값을 정하는 방법으로, 선형 회귀에서는 오차의 제곱 합 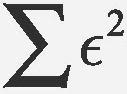이 최소가 되도록 회귀 계수를 정한다. 예를 들어, 단순 선형 회귀의 경우 다음을 최소로 만든다.

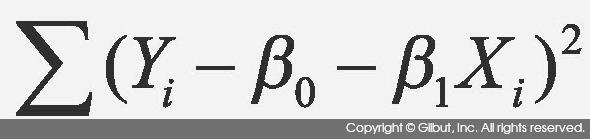
주어진 데이터에 선형 회귀 모델을 적합하고 나면 residuals( ) 함수를 사용해 잔차 를 구할 수 있다. 최소 제곱법으로 회귀 계수를 추정한다는 점 때문에 잔차의 제곱 합(RSS, Residual Sum of Squares)은 데이터와 추정된 모델 간의 불일치 정도를 표현하는 것으로 볼 수 있다.[4]