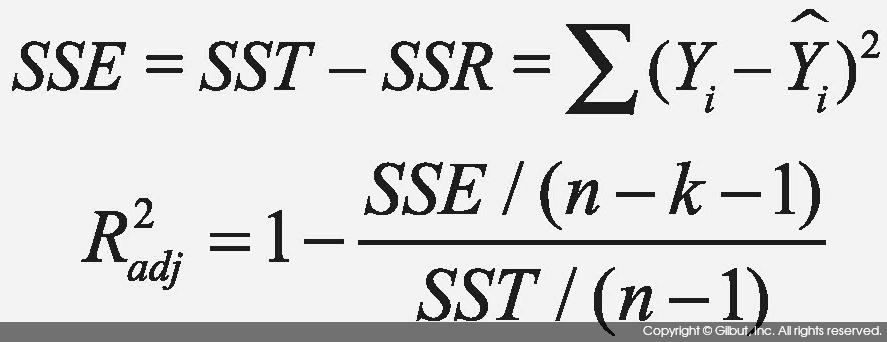결정 계수와 F 통계량

summary( )의 결과 중 다음 부분은 모델의 결정 계수와 F 통계량을 보여준다.

Residual standard error: 15.38 on 48 degrees of freedom
Multiple R-squared: 0.6511,     Adjusted R-squared: 0.6438
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

이 결과에서 결정 계수R-squared와 수정 결정 계수Adjusted R-squared는 각각 0.6511, 0.6438이었다. F 통계량F-statistic의 p-value는 1.49e-12였다. F 통계량은 MSR/MSE의 비율을 F 분포를 사용해 검정한 것이며, 이 값은 dist = β₀ + ε의 축소 모델reduced model과 dist = β₀ + β₁×speed + ε의 완전 모델full model 간에 잔차 제곱 합이 얼마나 유의하게 다른지 보는 방식과 같다. 다시 말해, F 통계량은 ‘H₀: β₁=0’, ‘H₁: β₁≠0’에 대한 가설 검정 결과다.[1], [5]

<Note> 결정 계수와 수정 결정 계수

---

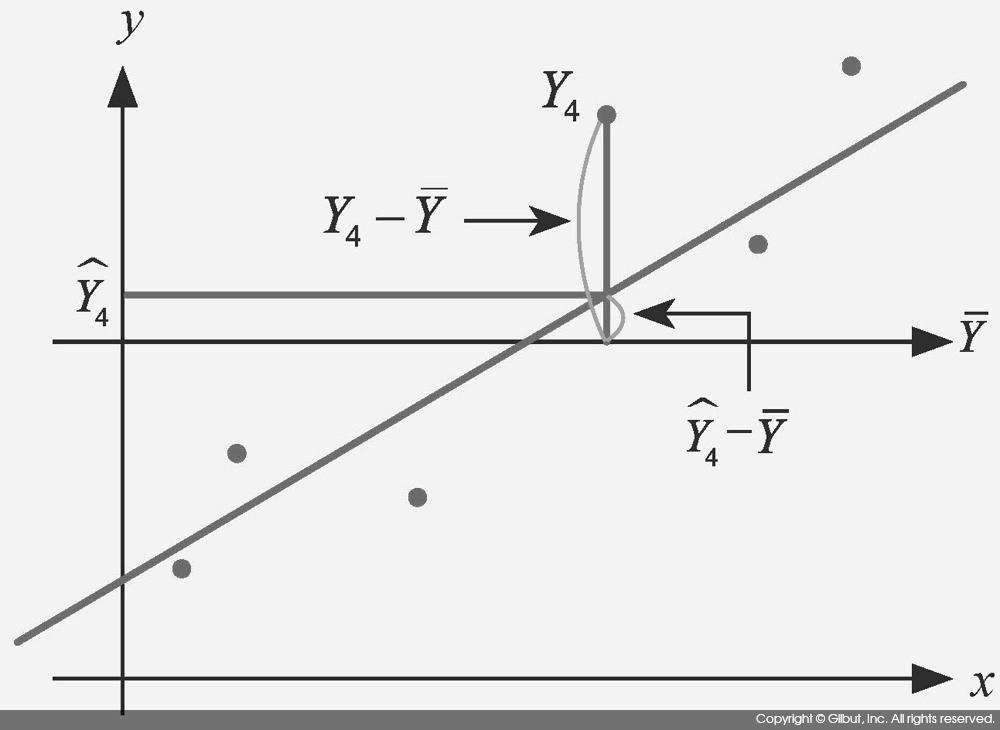
결정 계수(R-squared; R²으로도 표시)는 다음에 보인 식 8-3으로 정의된다.[1] 식에서 Y_i는 i번째 종속 변수의 값, 는 종속 변수 Y_i의 평균, 는 i번째 종속 변수의 값을 선형 회귀 모델로 예측한 값이다.

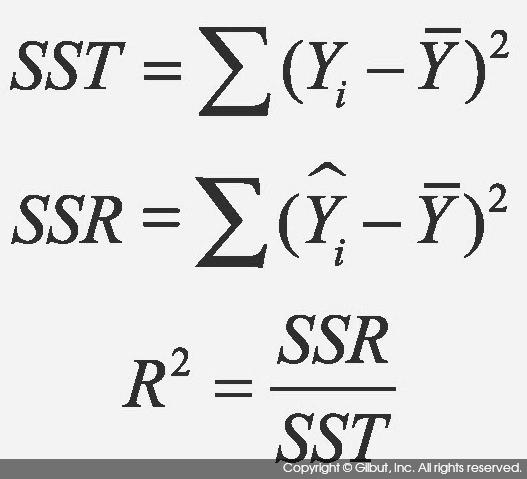
SST는 총 제곱 합(Total Sum of Squares), SSR은 회귀 제곱 합(Sum of Squares due to Regression)의 약어다. SST는 관측된 Y_i 값이 Y_i들의 평균 로부터 얼마나 떨어져 있는지를 뜻하며, SSR은 추정치 가 평균 로부터 얼마나 떨어져 있는지를 뜻한다. 따라서 이 둘의 비율인 R²은 Y_i의 총 변동에 대비해 회귀 모델이 얼마나 그 변동을 설명하는지를 알려준다. R²의 범위는 0 ≤ R² ≤ 1을 만족하며, 1에 가까울수록 회귀 모델이 데이터를 더 잘 설명한다고 할 수 있다. 그림 8-1은 를 보여준다.

R²은 독립 변수가 늘어나면 값이 커지는 성질이 있으므로, 서로 다른 개수의 독립 변수를 사용하는 모델 간의 비교에 사용하기에는 적합하지 않다. 따라서 R²을 자유도로 나눈 수정 결정 계수(Adjusted R-squared; R_adj²으로 표시)를 더 많이 사용한다. R_adj²은 다음과 같이 정의한다.

이 식에서 SSE는 잔차 제곱 합(Sum of squares due to residual erros)이라고 하며 SST = SSR + SSE의 관계를 가진다. R_adj²의 식에서 n은 데이터의 수, k는 독립 변수의 수이다.