좀 더 일반적으로 데이터의 상호 작용을 살펴보는 그림은 상호 작용 그래프interaction plot며, interaction.plot( )을 사용해 그릴 수 있다.

interaction.plot(
  x.factor,      # X 축에 그릴 팩터
  trace.factor,  # 자취를 그릴 레벨을 저장한 팩터
  response       # 반응값을 저장한 숫자 벡터
)

다음은 Orange 데이터에서 age, Tree의 상호 작용이 circumference에 어떤 영향을 주는지 알아보기 위해 상호 작용 그래프를 그린 예다.

> with(Orange, interaction.plot(age, Tree, circumference))

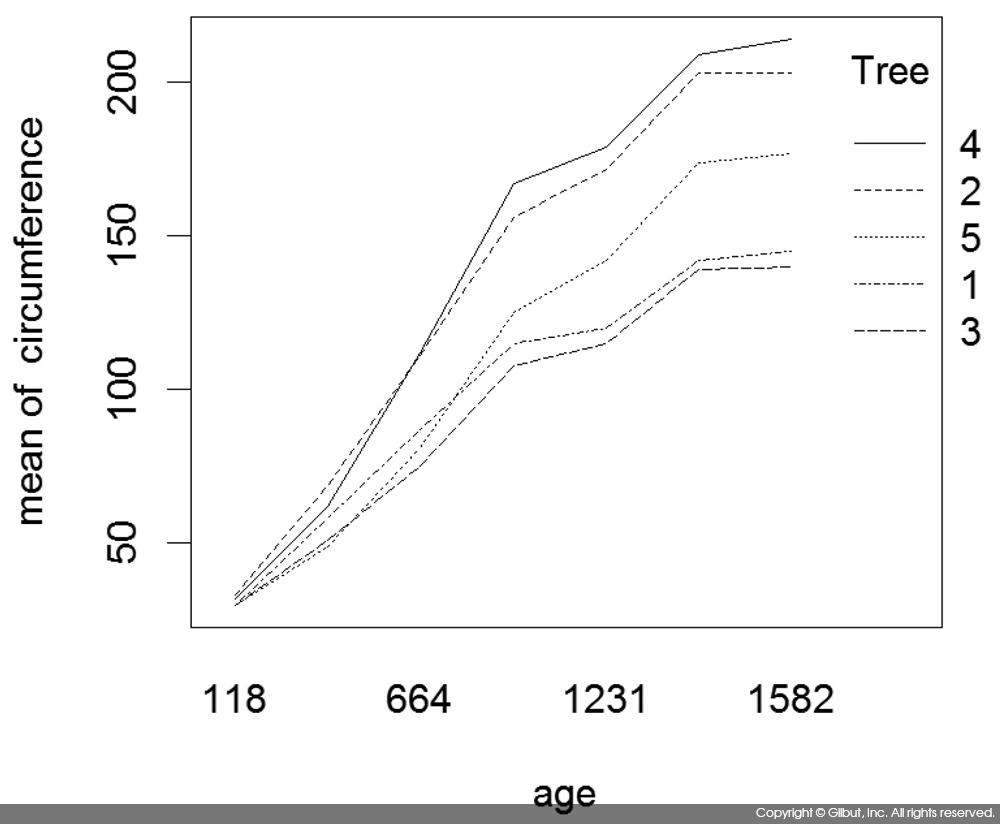
그림 8-9에서 볼 수 있듯이 나무의 수령이 높아짐에 따라 둘레가 길어지는 추세가 관찰되었다. 그리고 어떤 나무인가에 따라 수령과 둘레의 관계는 서로 다른 것으로 보인다.

lm( )을 사용해 선형 회귀를 수행해보자. 그러기 위해서는 Tree열을 수정할 필요가 있다. 이 절에서 다루고자 하는 내용은 범주형 변수와 연속형 변수의 상호 작용이다. 반면 Orange$Tree는 순서가 있는 범주형 변수Ordered Factor므로, 이를 순서가 없는 명목형 변수로 바꿔준다.

> Orange[,"fTree"] <- factor(Orange[, "Tree"], ordered=FALSE)

다음은 fTree, age, fTree:age를 설명 변수로 선형 회귀를 수행하는 코드다.

> m <- lm(circumference ~ fTree * age, data=Orange)
> anova(m)
Analysis of Variance Table

Response: circumference
          Df Sum Sq Mean Sq  F value     Pr(>F)
fTree      4  11841    2960  27.2983 8.428e-09 ***
age        1  93772   93772 864.7348 < 2.2e-16 ***
fTree:age  4   4043    1011   9.3206 9.402e-05 ***
Residuals 25   2711     108
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

보다시피 fTree, age 두 설명 변수가 모두 p 값이 0.05보다 작아 유의한 것으로 나타났다. 둘의 상호 작용인 fTree:age 역시 유의한 것으로 보인다.5

5 만약 fTree:age가 유의하지 않게 나타났다면 상호 작용을 제외하고 fTree + age의 포뮬러로 새로 회귀 분석을 수행해야 한다.