주성분 분석(PCA, Principal Component Analysis)
주성분 분석은 데이터에 많은 변수가 있을 때 변수의 수를 줄이는 차원 감소Dimensionality Reduction 기법 중 하나다. PCA는 변수들을 주성분Principal Component이라 부르는 선형적인 상관관계가 없는 다른 변수들로 재표현한다.2
주성분들은 원 데이터의 분산(퍼짐 정도)을 최대한 보존하는 방법으로 구한다.
주성분 분석이 어떻게 동작하는지 그림으로 살펴보자. 그림 9-7과 같이 데이터가 주어졌다고 하자.
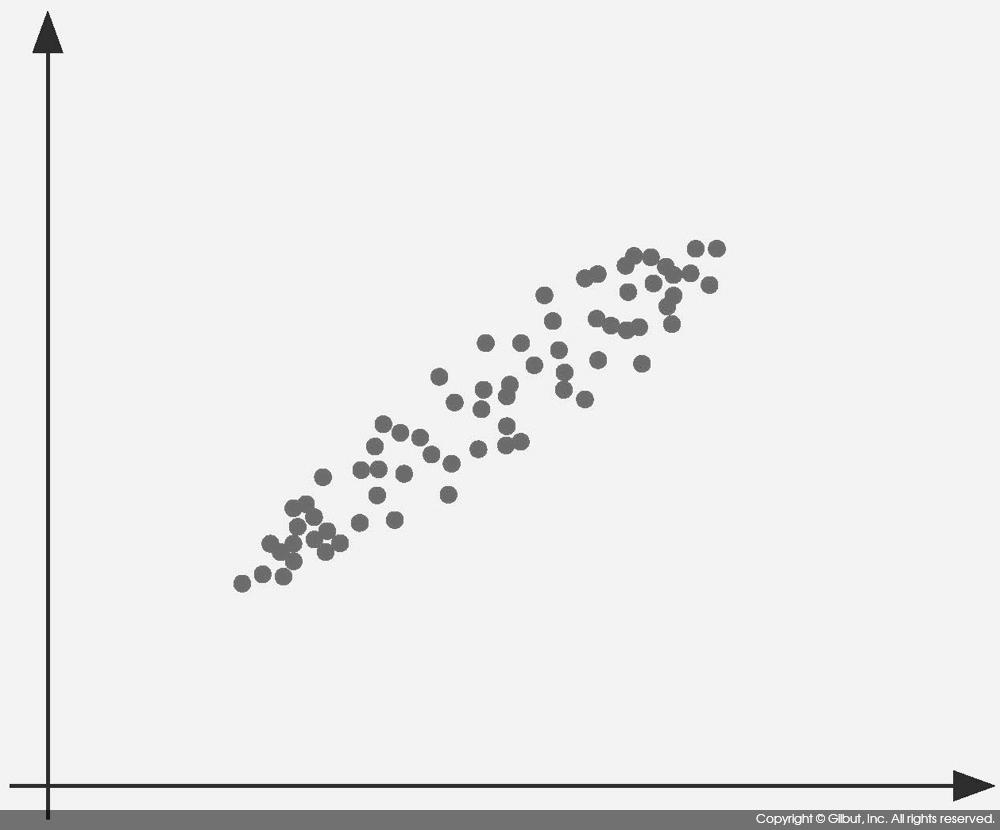
그림 9-7의 데이터는 X, Y 간 양의 상관관계가 관찰되는 데이터다. 주성분 분석이 구하는 첫 번째 주성분은 데이터의 분산을 가장 잘 표현하는 축(데이터가 가장 넓게 퍼진 축)이다. 이 데이터에서는 대각선 방향이 이에 해당한다. 즉, 그림 9-8에 보인 벡터다.
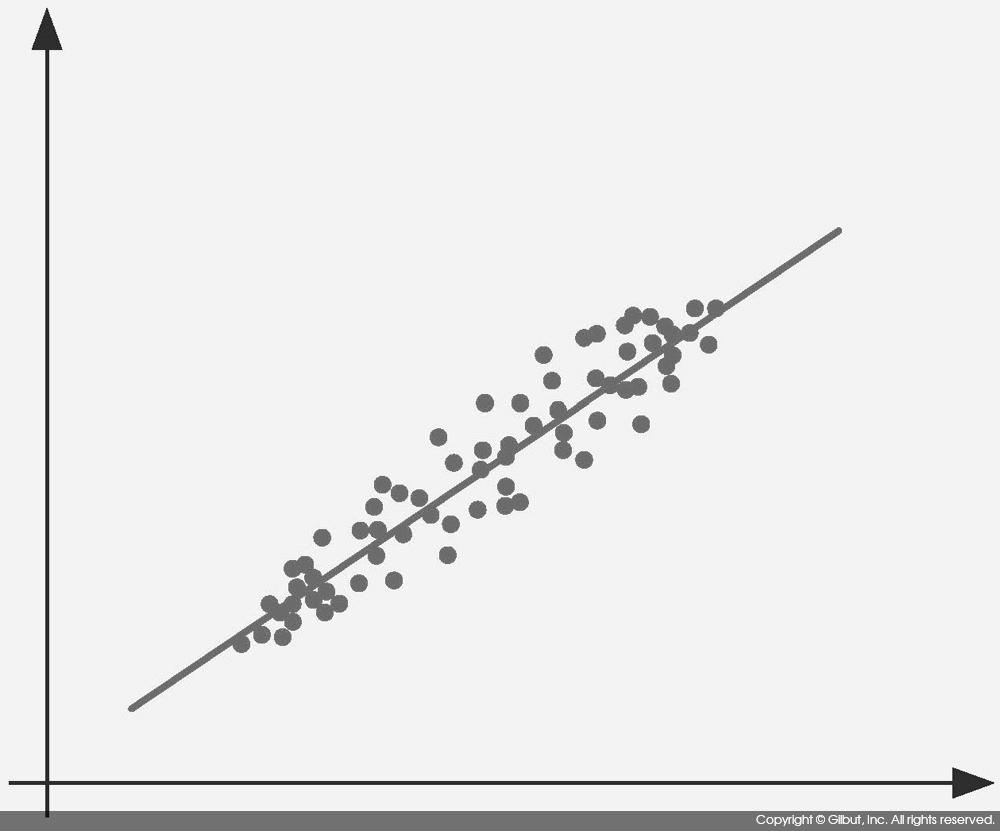
이렇게 새로운 축이 구해지면 데이터를 해당 축으로 표현하여 새로운 좌표를 부여할 수 있다. 이를 그림 9-9에 보였다.
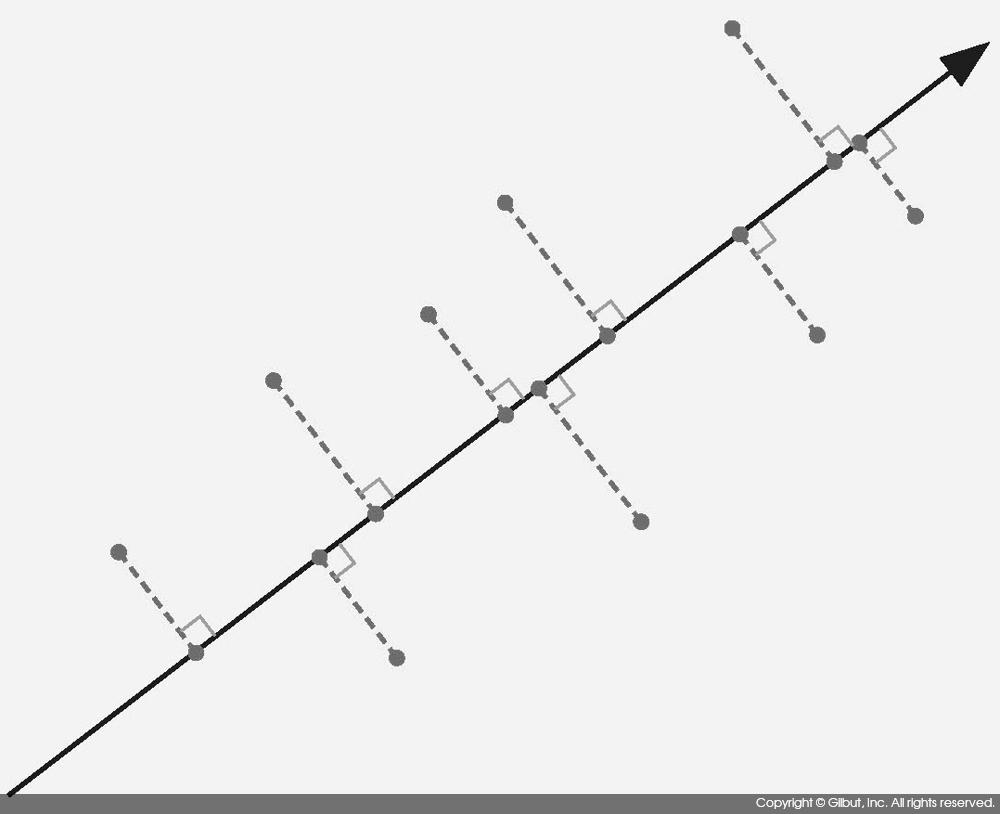
이제 첫 번째 주성분과 그 위에 데이터를 정사한 1차원의 좌표로 데이터를 재표현하게 되었다. 이 새로운 좌표가 첫 번째 주성분 점수다.
주성분 분석에서 구하는 두 번째 주성분은 첫 번째 주성분과 수직이면서 남아 있는 데이터의 분산을 가장 잘 표현하는 축이다. 이를 그림 9-10에 보였다.
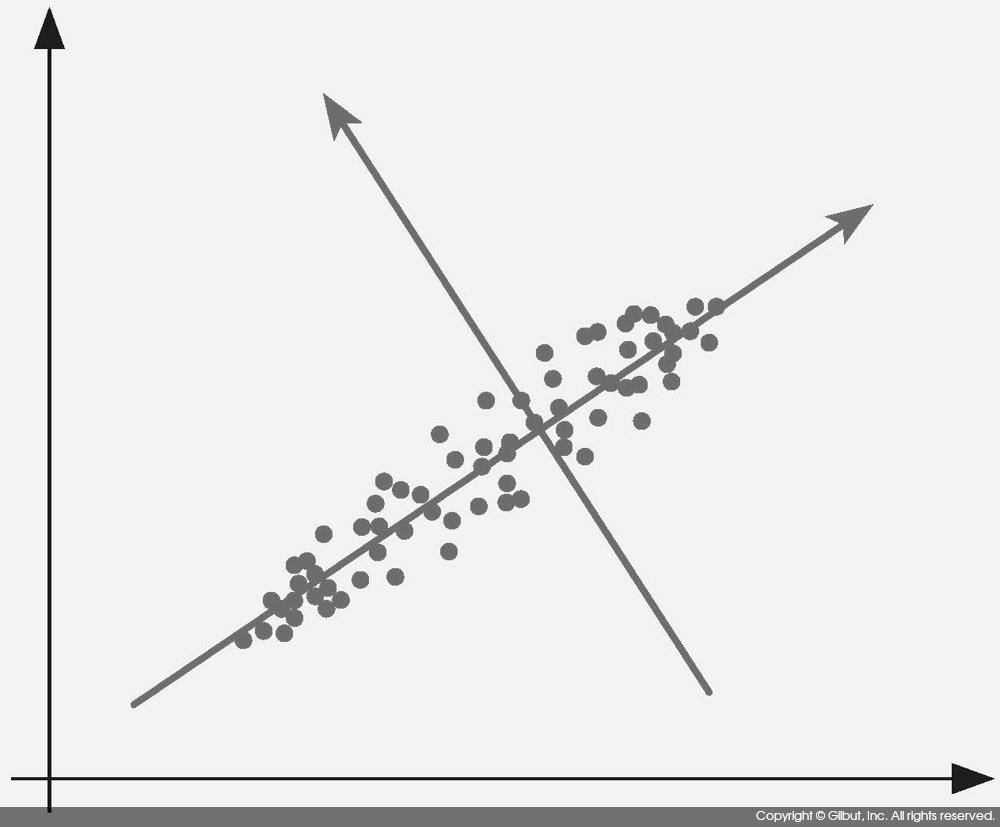
첫 번째 주성분의 경우와 마찬가지로 데이터를 두 번째 주성분의 좌표로 표현하면 두 번째 주성분 점수를 구하게 된다.
이처럼 주성분 분석은 데이터의 분산을 잘 표현하는 수직인 축들에 데이터를 정사한 좌표(주성분 점수)로 데이터를 재표현하며, 먼저 구해지는 주성분에 데이터의 분산이 더 많이 표현된다.
2 예를 들어, 변수 A, B로 변수 Y를 예측한다고 하자. 이때 A = 2×C + 3, B = 3×C와 같은 관계가 성립한다면 A, B 대신 C로 Y를 예측하는 것이 더 좋을 수 있다. 이처럼 PCA는 선형적으로 상관관계가 없는 독립된 변수들을 찾는 기법이다.