평가 메트릭

분류가 Y, N 두 종류가 있다고 할 때 분류 모델에서의 모델 평가 메트릭metric은 모델에서 구한 분류의 예측값과 데이터의 실제 분류인 실제 값의 발생 빈도를 나열한 그림 9-17의 혼동 행렬Confusion Matrix로부터 계산한다.[12], [13]

혼동 행렬에서 True Positive에 해당하는 셀은 실제 값이 Y고, 예측도 Y였던 경우의 수, False Positive는 실제 값은 N이었는데 예측이 Y로 된 경우의 수를 기록한다. 같은 방식으로 False Negative와 True Negative도 기록할 수 있다.

혼동 행렬의 각 셀에 붙은 이름은 True 또는 False에 이은 Positive 또는 Negative다. 이름에서 True와 False는 예측이 정확했는지를 뜻하며, Positive와 Negative는 예측값을 의미한다. 예를 들어, True Positive는 예측이 정확했고 이때 예측값은 Positive(즉, Y)였음을 뜻한다. 또 다른 예로 False Positive는 예측이 틀렸고 예측값은 Positive였음을 뜻한다. 예측이 틀린 경우므로 실제 분류는 Negative(즉, N)다.

혼동 행렬로부터 계산할 수 있는 가장 대표적인 메트릭은 다음과 같다.

메트릭	계산식	의미
Precision		Y로 예측된 것 중 실제로도 Y인 경우의 비율
Accuracy		전체 예측에서 (예측이 Y이든 N이든 무관하게) 옳은 예측의 비율
Recall (Sensitivity, TP Rate, Hit Rate로도 부름)		실제로 Y인 것들 중 예측이 Y로 된 경우의 비율
Specificity		실제로 N인 것들 중 예측이 N으로 된 경우의 비율
FP Rate (False Alarm Rate로도 부름)		Y가 아닌데 Y로 예측된 비율. 1-Specificity와 같은 값
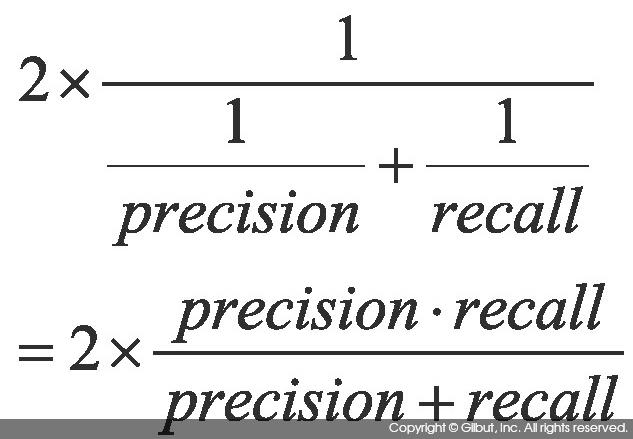
F1 점수[14]		Precision과 Recall의 조화 평균. 시스템의 성능을 하나의 수치로 표현하기 위해 사용하는 점수로, 0~1 사이의 값을 가진다. Precision과 Recall 중 한쪽만 클 때보다 두 값이 골고루 클 때 큰 값을 가진다.
Kappa[15]		코헨의 카파는 두 평가자의 평가가 얼마나 일치하는지 평가하는 값으로 0~1 사이의 값을 가진다. P(e)는 두 평가자의 평가가 우연히 일치할 확률을 뜻하며, 코헨의 카파는 두 평가자의 평가가 우연히 일치할 확률을 제외한 뒤의 점수다.

<Note> 코헨의 카파에서 P(e)의 계산

---

코헨의 카파에서 P(e)는 { (TP+FP) * (TP+FN) * (FN+TN) * (FP + TN) } / Total²으로 계산된다. 이때 Total = TP + FP + FN + TN이다.

이 식은 어떻게 유도할까? 그림 9-17을 예측값과 실제 값이 아닌 평가자 A와 평가자 B가 어떤 대상에 대해 내린 결론이라고 생각해보자. 그러면 평가자 A가 Y라는 평가를 줄 확률은 (TP + FP) / Total이다. 마찬가지로 평가자 B가 Y라는 평가를 내릴 확률은 (TP + FN) / Total이다. 따라서 A와 B가 우연히 Y라는 같은 평가를 내릴 확률은 이 둘의 곱인 (TP + FP) * (TP + FN) / Total²이다. 마찬가지로 평가자 A와 평가자 B가 우연히 N이라는 같은 평가를 내릴 확률은 (FN + TN) * (FP + TN) / Total²이다. 따라서 평가자 A와 평가자 B가 우연히 같은 평가를 내릴 확률은 이 둘의 합이다.