서포트 벡터 머신 모델의 핵심 수식은 벡터 간 내적 계산이다. 커널 트릭에서는 실제로 데이터를 고차원으로 변환하는 대신 고차원에서 벡터 간 내적 계산을 했을 때와 같은 값을 반환하는 함수들을 사용한다. 이 함수들을 사용하면 마치 데이터를 고차원으로 옮긴 듯한 효과를 일으키면서도 데이터를 고차원으로 옮기는 데 따른 계산 비용 증가는 피할 수 있다. 이러한 함수들을 커널 함수Kernel Function라고 부른다.

커널 함수의 대표적인 예에는 다항 커널Polynomial Kernel과 가우시안 커널Gaussian Kernel(레이디얼 베이스 함수 커널Radial Basis Function Kernel)이 있다. d차원 다항식에 대한 다항 커널[13]을 식 10-8에 보였다.

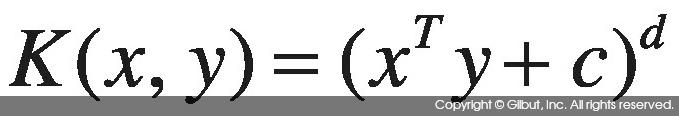
다항 커널은 입력의 모든 차원의 조합인 공간에서 내적을 계산한 것과 같은 결과를 반환한다. 예를 들어, 2차원 입력 벡터 x=(x1 x2)^T, y=(y1 y2)^T에 d=2인 다항 커널을 사용하면 다음 결과를 얻는다.

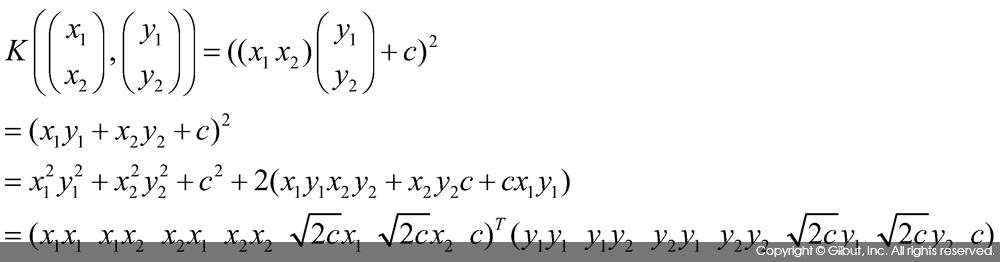
결국 식 10-8은 (x1 x2)^T을 다음에 보인 좌표로 옮긴 뒤 내적을 계산한 것과 같은 효과를 준다.

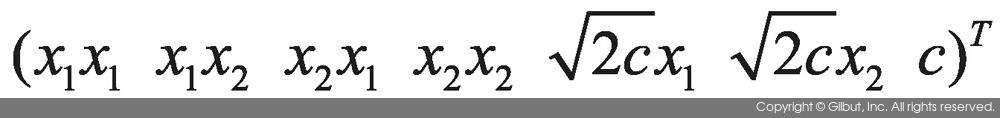
반면 가우시안 커널은 무한 차원으로 데이터를 옮긴 뒤 그곳에서 내적을 계산한 것과 같은 결과를 반환한다.3

가우시안 커널을 식 10-9에 보였다.

---

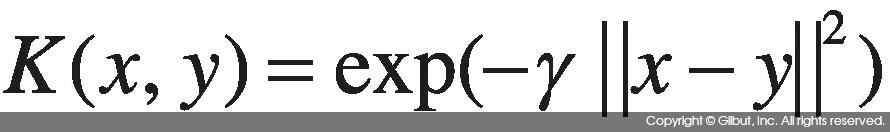
3 커널이 어떻게 차원을 옮긴 곳에서 내적을 계산하는지에 대해서는 참고자료 [14], [15]를 참고하기 바란다.