맥니마 검정
벌금을 부과하기 시작한 후 안전벨트 착용자의 수, 선거 유세를 하고 난 뒤 지지율의 변화와 같이 응답자의 성향이 사건 전후에 어떻게 달라지는지를 알아보는 경우 맥니마 검정McNemar Test을 수행한다.[9] 사건 전후에 응답자에게 설문을 하여 사건 발생 전 설문 결과를 Test1, 사건 발생 후 설문 결과를 Test2라고 명시한 다음 표8를 보자.
|
Test 2 양성(positive) |
Test 2 음성(negative) |
총계 |
|
|
Test 1 양성(positive) |
a |
b |
a + b |
|
Test 1 음성(negative) |
c |
d |
c + d |
|
총 계 |
a + c |
b + d |
n |
사건 전후에 설문 결과에 응답자 수 변화가 없다면 Test1의 positive와 Test2의 positive가 동일해야 하므로 a + b = a + c가 성립해야 한다. 또한, Test1의 negative와 Test2의 negative가 동일해야 하므로 c + d = b + d가 성립해야 한다. 이 둘을 정리해 결과적으로 b = c 여부를 검토하면 사건 전후에 성향 변화가 생겼는지 알 수 있다.
b = c가 성립하려면 b, c의 값이 b + c의 절반씩이 되어야 하므로 b는 이항 분포를 따른다.
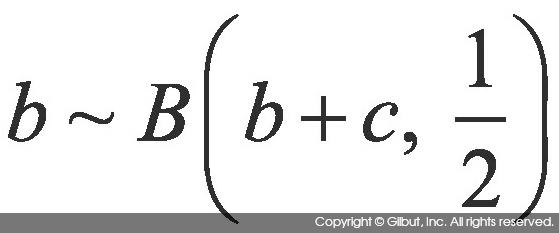
이항 분포는 B(n, p)로 표현하며 성공 가능성이 p로 일정하고 성공과 실패의
두 가지 결과만을 가진 실험(이를 베르누이 실험이라 한다)을 n회 수행할 때
총 성공 횟수의 분포를 나타낸다. 이항 분포의 확률 함수는 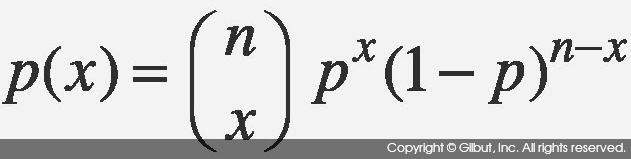 이다.
이다.
예를 들어, 동전을 던졌을 때 앞면이 나올 확률이 50%일 때 이 동전을 10번
던지는 시행은 B(10, 0.5)다. 10번 던져 앞면이 나온 수가 5가 될 확률은 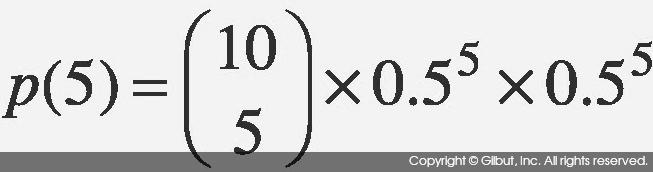 이다.
이다.
이항 분포 B(n, p)에서 n(앞서 설문 조사 표에서는 b + c에 해당)이 크다면 이항 분포를 정규 분포로 근사할 수 있다.
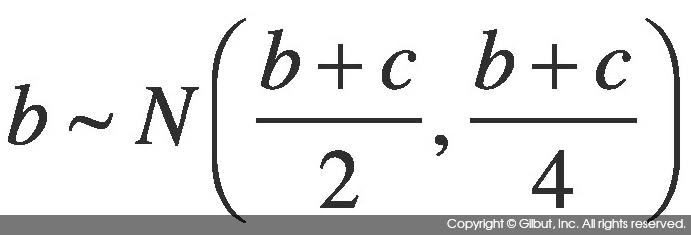
정규 분포는 평균 μ, 분산 σ2일 때 N(μ, σ2)으로 표현한다. 이항 분포 B(n, p)의 평균은 np, 분산은 np(q-p)므로 n이 클 때 B(n, p)는 N(p, np(1-p))로 근사할 수 있다.
b를 표준화하여 N(0, 1)을 따르게 하고 연속성 수정Continuity Correction을 하면 다음이 성립한다.[10]
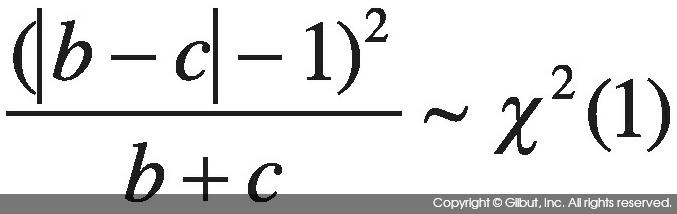
이제 ~의 좌측에 있는 통계량을 계산한 다음 이 값이 χ2(1)의 어디에 있는지를 보면 b=c인지 여부를 알 수 있다. 이를 수행해주는 R 함수는 mcnemar.test( )다. 또는 b가 b + c의 절반에 해당하는지를 이항 분포를 사용해 검정할 수도 있다. 이때 사용하는 함수는 binom.test( )다.
|
mcnemar.test : 맥니마 검정을 수행한다. |
mcnemar.test( x, # 행렬 형태의 이차원 분할표 또는 팩터 y=NULL, # 팩터. x가 행렬일 경우 무시 correct=TRUE # 연속성 수정 적용 여부 ) |
|
binom.test : 이항 분포 검정을 수행한다. |
binom.test( x, # 성공의 수. 또는 성공과 실패 수를 각각 저장한 길이 2인 벡터 n, # 시행 횟수. x의 길이가 2라면 무시 p=0.5, # 성공 확률에 대한 가설 alternative=c("two.sided", "less", "greater") # 대립 가설의 형태. 기본값은 양측 검정 ) |
8 맥니마 검정의 위키피디아 페이지(http://en.wikipedia.org/wiki/McNemar’s_test)의 그림을 인용했다.