평균이 0이고 표준 편차 σ가 각각 0.5, 1.0, 2.0인 가우시안 분포 그래프를 그림 7-8에 나타냈습니다. 세 개의 그래프가 모두 평균이 0이므로 x=0에서 최댓값을 가지며, x가 0에서 멀어질수록 함수 값이 감소합니다. 표준 편차 σ가 작으면 가우시안 분포 함수 그래프가 뾰족한 형태가 되고, 반대로 표준 편차 σ가 크면 그래프가 넓게 퍼지면서 완만한 형태를 따릅니다. 가우시안 분포 함수 값은 특정 x가 발생할 수 있는 확률의 개념을 가지며, 그래프 아래 면적을 모두 더하면 1이 됩니다.

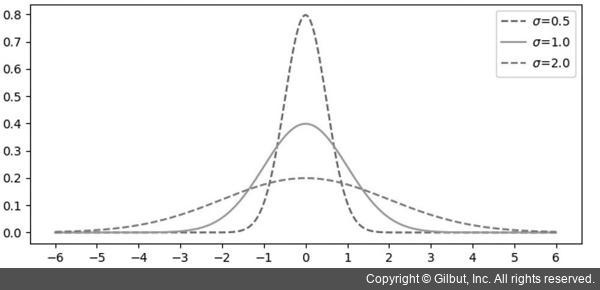
▲ 그림 7-8 평균이 0인 1차원 가우시안 분포 함수 그래프

 

가우시안 분포를 따르는 2차원 필터 마스크 행렬을 생성하려면 2차원 가우시안 분포 함수를 근사해야 합니다. 2차원 가우시안 분포 함수는 x와 y 두 개의 변수를 사용하고, 분포의 모양을 결정하는 평균과 표준 편차도 x축과 y축 방향에 따라 따로 설정합니다. 평균이 (0, 0)이고 x축과 y축 방향의 표준 편차가 각각 σ_x, σ_y인 2차원 가우시안 분포 함수는 다음과 같이 정의됩니다.