평균은 (0, 0)이고 σx=σy=1.0인 2차원 가우시안 분포 함수 그래프를 그림 7-9에 나타냈습니다. 2차원 가우시안 분포 함수 그래프는 1차원 가우시안 분포 함수 그래프의 차원을 확장한 형태입니다. 평균이 (0, 0)이므로 그림 7-9 그래프는 (0, 0)에서 최댓값을 갖고, 평균에서 멀어질수록 함수가 감소합니다. 2차원 가우시안 분포 함수의 경우, 함수 그래프 아래의 부피를 구하면 1이 됩니다.
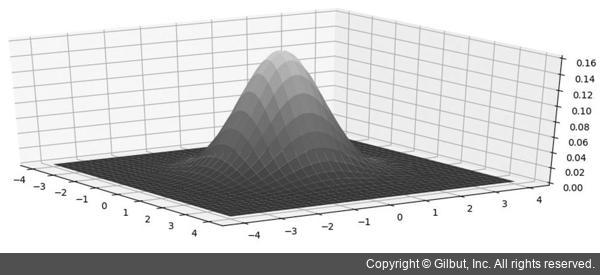
▲ 그림 7-9 평균이 (0, 0)인 2차원 가우시안 함수 그래프(σx=σy=1.0)
가우시안 필터는 이러한 2차원 가우시안 분포 함수로부터 구한 마스크 행렬을 사용합니다. 가우시안 분포 함수는 연속 함수이지만 이산형의 마스크를 만들기 위해서 x와 y 값이 정수인 위치에서만 가우시안 분포 함수 값을 추출하여 마스크를 생성합니다. 평균이 0이고 표준 편차가 σ인 가우시안 분포는 x가 -4σ부터 4σ 사이인 구간에서 그 값의 대부분이 존재하기 때문에 가우시안 필터 마스크의 크기는 보통 (8σ+1)로 결정합니다.3 예를 들어 그림 7-9와 같이 σx=σy=1.0인 가우시안 함수를 사용할 경우, x={-4, -3, -2, -1, 0, 1, 2, 3, 4}, y={-4, -3, -2, -1, 0, 1, 2, 3, 4}인 경우에만 가우시안 분포 함수 값을 추출하여 필터 마스크를 생성합니다. 이러한 방식으로 추출한 9×9 가우시안 필터 마스크를 그림 7-10에 나타냈습니다.4

▲ 그림 7-10 σx=σy=1.0인 경우의 가우시안 필터 마스크
3 예외적으로 CV_8U 깊이의 영상에 대해 가우시안 필터를 적용하면 (6σ+1) 크기의 필터 마스크를 사용합니다. 만약 필터 마스크 크기를 반올림하여 만든 정수 값이 짝수이면 1을 더하여 홀수로 만듭니다.
4 정수 좌표에서 가우시안 분포 함수 값을 선택하여 가우시안 필터 마스크를 만든 후, 필터 마스크 행렬 원소 합이 1이 되도록 행렬 원소 값의 크기를 전체적으로 조정해야 합니다.