앞 수식에서 여섯 개의 파라미터로 구성된 2×3 행렬 를 어파인 변환 행렬(affine transformation matrix)이라고 부릅니다. 즉, 어파인 변환은 2×3 실수형 행렬 하나로 표현할 수 있습니다.

입력 영상과 어파인 변환 결과 영상으로부터 어파인 변환 행렬을 구하기 위해서는 최소 세 점의 이동 관계를 알아야 합니다. 점 하나의 이동 관계로부터 x 좌표와 y 좌표에 대한 변환 수식 두 개를 얻을 수 있으므로, 점 세 개의 이동 관계로부터 총 여섯 개의 방정식을 구할 수 있습니다. 그러므로 점 세 개의 이동 관계를 알고 있다면 여섯 개의 원소로 정의되는 어파인 변환 행렬을 구할 수 있습니다.

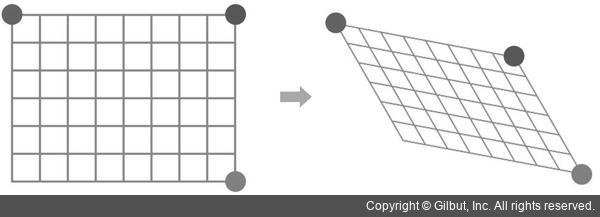
그림 8-2는 점 세 개의 이동 관계에 의해 결정되는 어파인 변환을 보여 줍니다. 그림 8-2에서 왼쪽 직사각형 꼭지점 세 개를 빨간색, 보라색, 녹색으로 표시하였고, 이 점들이 이동한 위치를 그림 8-2 오른쪽 그림에 같은 색상으로 나타냈습니다. 어파인 변환에 의해 직사각형 영상은 평행사변형 형태로 변환될 수 있기 때문에 입력 영상의 좌측 하단 모서리 점이 이동하는 위치는 자동으로 결정됩니다. 그러므로 어파인 변환은 점 세 개의 이동 관계만으로 정의할 수 있습니다.

▲ 그림 8-2 어파인 변환