1차원 연속 함수 f(x)의 값 변화에 따른 미분 f′(x)를 그림 9-1에 나타냈습니다. 그림 9-1(a)는 함수 f(x)의 그래프이고, 그림 9-1(b)는 f(x)를 미분한 f′(x)의 그래프입니다. 그림 9-1(a)에서 함수 그래프가 수평으로 진행되는 부분은 함수 값 변화가 없는 부분이고, 이 위치에서의 f′(x) 값은 0입니다. 함수 f(x) 값이 급격하게 증가하는 ⓐ 위치에서는 f′(x) 값이 0보다 큰 값을 가집니다. f(x) 값이 급격하게 감소하는 ⓑ 위치에서는 f′(x) 값이 0보다 훨씬 작은 음수로 나타납니다. ⓒ 위치에서는 f(x) 값이 대체로 일정한 기울기로 증가하므로 f′(x) 값은 0보다 큰 양수 값이 일정하게 나타납니다. 그러므로 함수 f(x) 값이 급격하게 바뀌는 부분을 찾기 위해서는 함수의 미분 f′(x) 값이 0보다 훨씬 크거나 또는 훨씬 작은 위치를 찾아야 합니다.

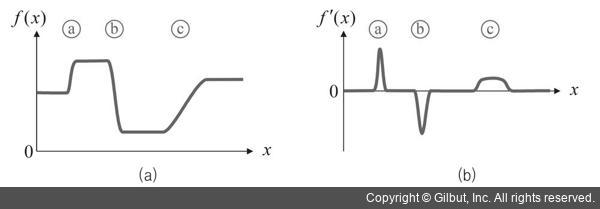
▲ 그림 9-1 1차원 연속 함수의 미분

 

잘 알려진 다항함수나 삼각함수 등의 미분을 계산하는 것은 이미 수학의 미적분학에서 많이 연구되었기 때문에 공식을 통해 쉽게 구할 수 있습니다. 그러나 영상은 2차원 평면 위에 픽셀 값이 정형화되지 않은 상태로 나열되어 있는 형태이므로 미분 공식을 적용할 수 없습니다. 영상으로부터 미분을 계산하려면 두 가지 특징을 고려해야 합니다. 하나는 영상이 2차원 평면에서 정의된 함수라는 점이고, 두 번째는 영상이 정수 단위 좌표에 픽셀이 나열되어 있는 이산함수라는 점입니다.