영상의 미분을 곧바로 설명하기에 앞서 먼저 1차원 이산함수에서 미분을 구하는 방법에 대해 알아보겠습니다. 영상과 같이 일련의 데이터가 순서대로 나열되어 있는 경우에는 미분 근사화 방법을 이용하여 변화량을 측정할 수 있습니다. 미분 근사는 다음 세 가지 방법을 주로 사용합니다.

• 전진 차분(forward difference):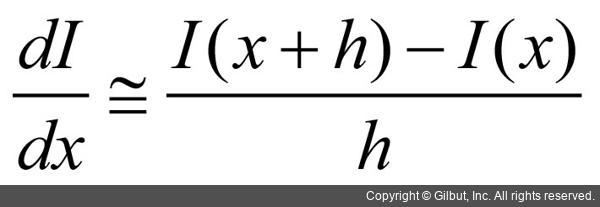

• 후진 차분(backward difference):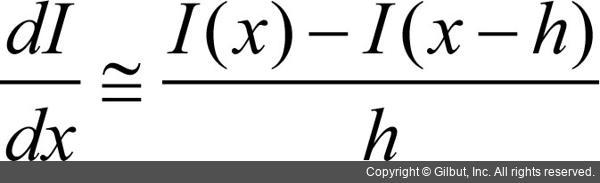

• 중앙 차분(centered difference):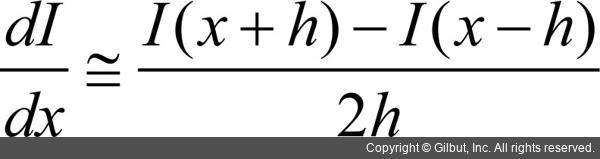

앞 수식에서 I(x)는 1차원 이산함수이고, h는 이산 값의 간격을 의미합니다. 미분 근사 방법을 영상에 적용할 경우, h는 픽셀의 간격이라고 생각할 수 있으며 보통 픽셀 간격의 최소 단위인 1을 h 값으로 사용합니다. 즉, 전진 차분 수식은 I(x+1)-I(x)로 정리되며, 이는 자기 자신 바로 앞에 있는 픽셀에서 자기 자신 픽셀 값을 뺀 형태입니다. 후진 차분은 I(x+1)-I(x)로 정리되며, 이는 자기 자신 픽셀에서 바로 뒤에 있는 픽셀 값을 뺀 형태입니다. 마지막으로 중앙 차분은 (I(x+1)-I(x-1))/2 수식으로 정리되며, 자기 자신을 제외하고 바로 앞과 뒤에 있는 픽셀 값을 이용하는 미분 근사 방법입니다. 세 가지 미분 근사 방법 중에서 중간값 차이를 이용하는 방법이 이론적으로 근사화 오류가 가장 적으며, 실제 영상에서 미분을 계산할 때에도 널리 사용되고 있습니다.