영상은 2차원 평면에서 정의된 함수이기 때문에 영상에서 에지를 찾기 위해서는 영상을 가로 방향과 세로 방향으로 각각 미분해야 합니다. 2차원 영상 I(x, y)를를 가로 방향으로 미분한다는 것은 y 좌표는 고정한 상태에서 x축 방향으로만 미분 근사를 계산하는 것을 의미하며, 이러한 연산을 x축 방향으로의 편미분(partial derivative)이라고 합니다. x축 방향의 편미분은 I_x 또는 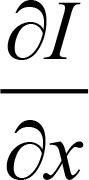로 표기합니다. 이와 유사하게 y축 방향으로의 편미분은 I_y 또는 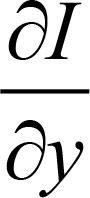라고 표기하고, x 좌표를 고정한 상태에서 y축 방향으로 미분 근사를 수행하여 구할 수 있습니다. 2차원 영상 I(x, y)에 대하여 x축과 y축 방향에 대한 각각의 편미분을 중앙 차분 방법으로 근사화하면 다음과 같습니다.

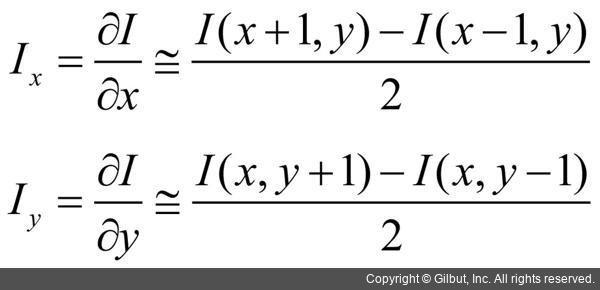
중앙 차분을 이용한 영상의 미분 근사는 마스크 연산을 이용하여 쉽게 구현할 수 있습니다. 2차원 영상을 x축과 y축 방향에 대해 편미분을 수행하는 필터 마스크를 그림 9-2에 나타냈습니다. 그림 9-2(a)는 영상을 x축 방향으로 편미분을 수행하는 1×3 필터 마스크이고, 그림 9-2(b)는 영상을 y축 방향으로 편미분하는 3×1 필터 마스크입니다. 앞서 설명한 편미분 근사 수식을 그대로 적용하려면 필터 마스크 값에 1/2을 곱해야 하지만 보통 미분 값의 상대적 크기를 중요시하기 때문에 그림 9-2와 같이 단순화시킨 마스크를 주로 사용합니다. 그림 9-2의 마스크를 이용하여 영상을 각각 필터링하면 영상을 가로 방향과 세로 방향으로 편미분한 정보를 담고 있는 행렬을 얻을 수 있습니다.

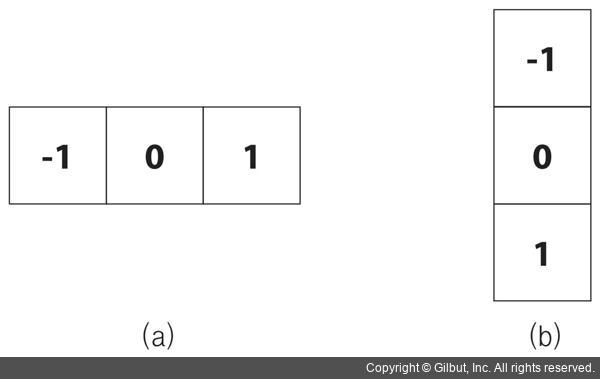
▲ 그림 9-2 중앙 차분에 의한 미분 근사 마스크