xy 좌표 공간과 ab 좌표 공간과의 관계를 제대로 이해하기 위해 그림 9-11을 살펴보겠습니다. 그림 9-11(a)에서 파란색 실선은 xy 공간에서 정의된 직선 y=a0x+b0입니다. 이 수식에서 a0와 b0는 직선의 모양을 결정하는 상수입니다. xy 공간에서 직선상의 한 점 (x0, y0)를 선택하고, 이 점의 좌표를 이용하면 ab 공간에서 빨간색 직선 b=-x0a+y0를 정의할 수 있습니다. 마찬가지로 xy 공간에서 직선상의 다른 한 점 (x1, y1)을 이용하면 ab 공간에서 보라색 직선 b=-x1a+y1을 표현할 수 있습니다. 이 경우 ab 공간에서 빨간색 직선과 보라색 직선이 서로 교차하는 점의 좌표는 (a0, b0)이며, 이는 xy 공간에서 직선의 방정식 y=a0x+b0를 정의하는 두 개의 파라미터로 구성된 좌표입니다. 즉, xy 공간에서 파란색 직선상의 점을 이용하여 생성한 ab 공간상의 직선들은 모두 (a0, b0) 점을 지나갑니다.
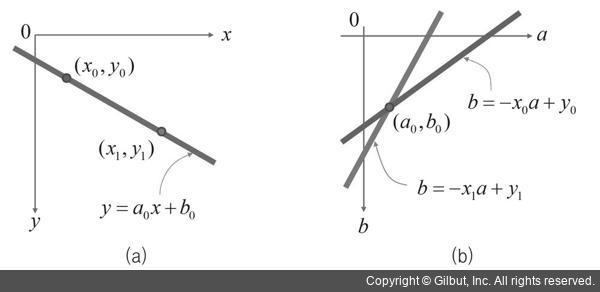
▲ 그림 9-11 xy 공간에서 ab 파라미터 공간으로 허프 변환
허프 변환을 이용하여 직선의 방정식을 찾으려면 xy 공간에서 에지로 판별된 모든 점을 이용하여 ab 파라미터 공간에 직선을 표현하고, 직선이 많이 교차되는 좌표를 모두 찾아야 합니다. 이때 직선이 많이 교차하는 점을 찾기 위해서 보통 축적 배열(accumulation array)을 사용합니다. 축적 배열은 0으로 초기화된 2차원 배열에서 직선이 지나가는 위치의 배열 원소 값을 1씩 증가시켜 생성합니다.