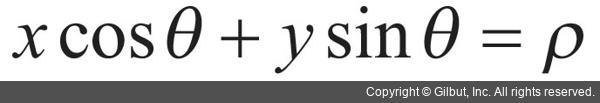그림 9-12는 허프 변환에서 축적 배열을 구축하는 방법을 보여 줍니다. 그림 9-12의 왼쪽 xy 영상 좌표계에서 직선 위 세 개의 점을 선택하였고, 각 점에 대응되는 ab 파라미터 공간에서의 직선을 오른쪽 배열 위에 나타냈습니다. 그리고 배열 위에서 직선이 지나가는 위치의 원소 값을 1씩 증가시킨 결과를 숫자로 나타냈습니다. 그림 9-12에서 오른쪽에 나타난 배열이 축적 배열이며, 축적 배열에서 최댓값을 갖는 위치에 해당하는 a와 b 값이 xy 공간에 있는 파란색 직선의 방정식 파라미터입니다. 그림 9-12에서는 하나의 직선에 대해 허프 변환 예를 설명하였으며, 여러 개의 직선이 존재하는 영상이라면 축적 배열에서 여러 개의 국지적 최댓값 위치를 찾아서 직선의 방정식 파라미터를 결정할 수 있습니다.

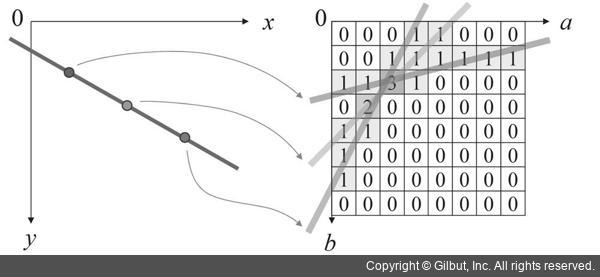
▲ 그림 9-12 2차원 영상 공간에서 파라미터 공간으로 변환

 

그러나 y=ax+b 형태의 직선의 방정식을 사용할 경우 모든 형태의 직선을 표현하기 어렵다는 단점이 있습니다. 대표적으로 y=ax+b 수식은 y축과 평행한 수직선을 표현할 수 없습니다. 수직선을 표현하려면 기울기 a 값이 무한대가 되어야 하기 때문입니다. 그러므로 실제 허프 변환을 구현할 때에는 다음과 같이 극좌표계 형식의 직선의 방정식을 사용합니다.