앞 수식에서 w(x, y)는 균일한 값을 갖는 사각형 윈도우 또는 가우시안 형태의 가중치를 갖는 윈도우입니다. 만약 E(Δx, Δy) 함수가 모든 방향으로 값이 크게 나타난다면 점 (x, y)는 코너라고 간주할 수 있습니다. 해리스는 E(Δx, Δy)가 모든 방향으로 그 값이 크게 나타나는지를 검사하기 위해 테일러 급수(Taylor series), 고윳값 분석(eigenvalue analysis) 등의 수학적 기법을 적용하여 코너 응답 함수 R을 유도하였습니다.

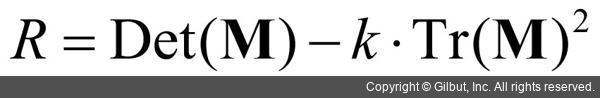
앞 수식에서 Det()는 행렬식(determinant)을, Tr()은 대각합(trace)을 의미하고, 행렬 M은 다음과 같이 정의됩니다.

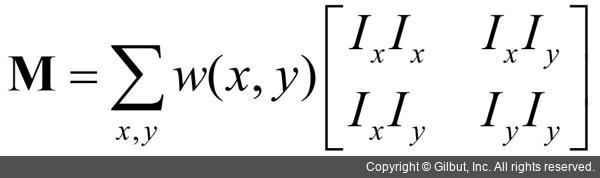
앞 수식에서 I_x와 I_y는 입력 영상 I를 각각 x축 방향과 y축 방향으로 편미분한 결과입니다. 코너 응답 함수 정의에서 상수 k는 보통 0.04~0.06 사이의 값을 사용합니다.

해리스에 의해 정의된 코너 응답 함수 R은 입력 영상 각각의 픽셀에서 정의되는 실수 값이며, 이 값을 분석하여 코너, 에지, 평탄한 영역을 판별할 수 있습니다. 만약 R이 0보다 충분히 큰 양수이면 코너 점이라고 간주합니다. 반면에 R이 0에 가까운 실수이면 평탄한 영역이고, 0보다 작은 음수이면 에지라고 판별합니다.