3.3.1 로지스틱 회귀의 이해와 조건부 확률
로지스틱 회귀는 구현하기 매우 쉽고 선형적으로 구분되는 클래스에 뛰어난 성능을 내는 분류 모델입니다. 산업계에서 가장 널리 사용되는 분류 알고리즘 중 하나입니다. 퍼셉트론이나 아달린과 마찬가지로 로지스틱 회귀 모델도 이진 분류를 위한 선형 모델입니다.9
Note ≡ 다중 클래스를 위한 로지스틱 회귀
로지스틱 회귀는 손쉽게 다중 클래스 설정으로 일반화할 수 있습니다. 이를 다항 로지스틱 회귀(multinomial logistic regression) 또는 소프트맥스 회귀(softmax regression)라고 부릅니다. 다항 로지스틱 회귀에 대한 자세한 내용은 이 책의 범위를 넘어섭니다. 관심 있는 독자는 제 강의 노트에서 자세한 정보를 확인하세요.10 https://sebastianraschka.com/pdf/lecture-notes/stat479ss19/L08_logistic_slides.pdf 또는 http://rasbt.github.io/mlxtend/user_guide/classifier/SoftmaxRegression/
다중 클래스 환경에서 로지스틱 회귀를 사용하는 또 다른 방법은 앞서 언급한 OvR 기법입니다.
이진 분류를 위한 확률 모델로서 로지스틱 회귀 모델 이면에 있는 아이디어를 설명하기 위해 먼저 오즈비(odds ratio)를 소개합니다. 오즈는 특정 이벤트가 발생할 확률입니다. 오즈비는 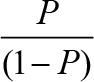 처럼 쓸 수 있습니다. 여기서 P는 양성 샘플일 확률입니다. 양성 샘플은 좋은 것을 의미하지 않고 예측하려는 대상을 말합니다. 예를 들어 환자가 어떤 질병을 가지고 있을 확률입니다. 양성 샘플이 클래스 레이블 y=1인 샘플입니다. 오즈비에 로그 함수(로그 오즈)를 취해 로짓(logit) 함수를 정의합니다.
처럼 쓸 수 있습니다. 여기서 P는 양성 샘플일 확률입니다. 양성 샘플은 좋은 것을 의미하지 않고 예측하려는 대상을 말합니다. 예를 들어 환자가 어떤 질병을 가지고 있을 확률입니다. 양성 샘플이 클래스 레이블 y=1인 샘플입니다. 오즈비에 로그 함수(로그 오즈)를 취해 로짓(logit) 함수를 정의합니다.
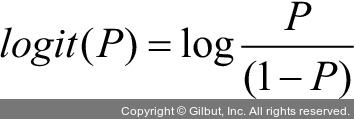
9 역주 잠시 후에 설명하지만 사이킷런의 로지스틱 회귀 구현은 다중 분류도 지원합니다.
10 역주 <핸즈온 머신러닝 2판>(한빛미디어, 2020)의 4장에서 소프트맥스 회귀에 대한 자세한 내용을 볼 수 있습니다.