z가 무한대로 가면(z→∞) e^-z가 매우 작아지기 때문에 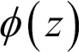는 1에 가까워집니다. 비슷하게 z→-∞이면 점점 분모가 커지기 때문에 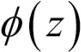는 0에 수렴합니다. 이 시그모이드 함수는 실수 입력 값을 [0, 1] 사이의 값으로 변환합니다. 중간은 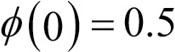입니다.

로지스틱 회귀 모델을 직관적으로 이해하기 위해 2장과 연관 지어 생각해 보겠습니다. 아달린에서 활성화 함수로 항등 함수 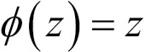를 사용했습니다. 로지스틱 회귀에서는 앞서 정의한 시그모이드 함수가 활성화 함수가 됩니다.

아달린과 로지스틱 회귀의 차이점을 그림 3-3에 나타냈습니다.

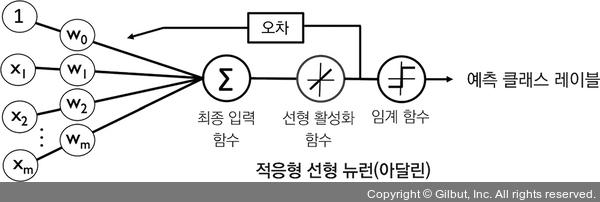
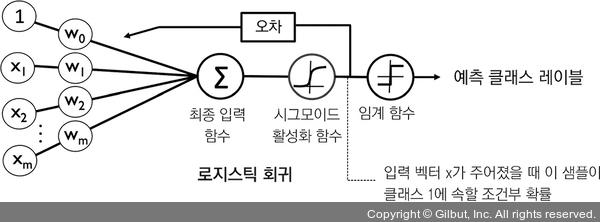
▲ 그림 3-3 아달린과 로지스틱 회귀의 차이점

가중치 w와 곱해지는 특성 x에 대한 시그모이드 함수의 출력을 특정 샘플이 클래스 1에 속할 확률 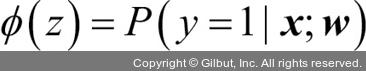로 해석합니다. 예를 들어 어떤 붓꽃 샘플이 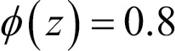이라면 이 샘플은 Iris-versicolor일 확률이 80%란 뜻입니다.