3.3.2 로지스틱 비용 함수의 가중치 학습
로지스틱 회귀 모델이 확률과 클래스 레이블을 어떻게 예측하는지 배웠습니다. 이제 모델 파라미터 w를 어떻게 학습하는지 간단하게 살펴보겠습니다. 이전 장에서 다음과 같은 제곱 오차합 비용 함수를 정의했습니다.

아달린 분류 모델에서 이 함수를 최소화하는 가중치 w를 학습합니다. 로지스틱 회귀의 비용 함수를 유도하는 방법을 설명하기 위해 먼저 로지스틱 회귀 모델을 만들 때 최대화하려는 가능도(likelihood) L을 정의하겠습니다. 데이터셋에 있는 각 샘플이 서로 독립적이라고 가정합니다. 공식은 다음과 같습니다.11

실전에서는 이 공식의 (자연) 로그를 최대화하는 것이 더 쉽습니다. 이 함수를 로그 가능도 함수라고 합니다.
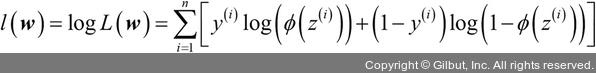
첫째, 로그 함수를 적용하면 가능도가 매우 작을 때 일어나는 수치상의 언더플로(underflow)를 미연에 방지합니다. 둘째, 계수의 곱을 계수의 합으로 바꿀 수 있습니다. 미적분을 기억하고 있을지 모르지만 이렇게 하면 도함수를 구하기 쉽습니다.
경사 상승법 같은 최적화 알고리즘을 사용하여 이 로그 가능도 함수를 최대화할 수 있습니다. 또는 로그 가능도 함수를 다시 비용 함수 J로 표현하여 2장처럼 경사 하강법을 사용하여 최소화할 수 있습니다.

11 역주 ∏ 기호는 수열의 곱(https://bit.ly/2NDA1zn)을 나타냅니다. 여기서는 n개의 샘플이 해당 클래스에 속할 확률을 곱한 것입니다. 양성 샘플일 경우 1-y(i)가 0이 되어 두 번째 항이 1이 되고 양성 샘플일 확률 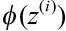 만 남습니다. 반대로 음성 샘플일 경우 y(i)가 0이 되어 첫 번째 항이 1이 되고 음성 샘플일 확률
만 남습니다. 반대로 음성 샘플일 경우 y(i)가 0이 되어 첫 번째 항이 1이 되고 음성 샘플일 확률  만 남습니다. 따라서 가능도가 최대가 되려면 양성 샘플의
만 남습니다. 따라서 가능도가 최대가 되려면 양성 샘플의 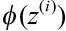 는 가능한 크고 음성 샘플의
는 가능한 크고 음성 샘플의 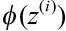 는 가능한 작아야 합니다.
는 가능한 작아야 합니다.