3.3.5 규제를 사용하여 과대적합 피하기
과대적합(overfitting)은 머신 러닝에서 자주 발생하는 문제입니다. 모델이 훈련 데이터로는 잘 동작하지만 본 적 없는 데이터(테스트 데이터)로는 잘 일반화되지 않는 현상입니다. 모델이 과대적합일 때 분산이 크다고 말합니다. 모델 파라미터가 너무 많아 주어진 데이터에서 너무 복잡한 모델을 만들기 때문입니다. 비슷하게 모델이 과소적합(underfitting)일 때도 있습니다(편향이 큽니다). 훈련 데이터에 있는 패턴을 감지할 정도로 충분히 모델이 복잡하지 않다는 것을 의미합니다. 이 때문에 새로운 데이터에서도 성능이 낮을 것입니다.
지금까지 분류를 위한 선형 모델만 보았지만 과대적합과 과소적합 문제는 그림 3-7과 같이 선형 결정 경계와 복잡한 비선형 결정 경계를 비교해서 설명하는 것이 좋습니다.
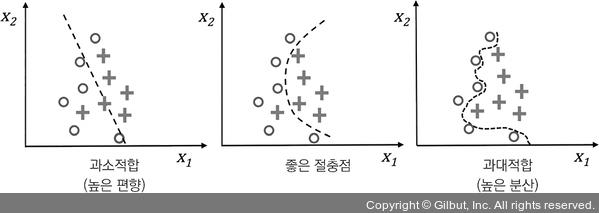
▲ 그림 3-7 과대적합과 과소적합이 결정 경계에 미치는 영향
Note ≡ 편향-분산 트레이드오프
연구자들은 종종 ‘편향(bias)’과 ‘분산(variance)’ 또는 ‘편향-분산 트레이드오프(tradeoff)’란 용어를 사용하여 모델의 성능을 설명합니다. 모델의 ‘분산이 높다’ 또는 ‘편향이 크다’고 말하는 대화, 책, 글을 보았을지 모릅니다. 이것은 무슨 뜻일까요? 일반적으로 ‘높은 분산’은 과대적합에 비례하고 ‘높은 편향’은 과소적합에 비례합니다.
머신 러닝 모델에서 분산은 모델을 여러 번 훈련했을 때 특정 샘플에 대한 예측의 일관성(또는 변동성)을 측정합니다. 예를 들어 훈련 데이터셋의 일부분을 사용하여 여러 번 훈련하는 경우입니다. 이런 모델은 훈련 데이터의 무작위성에 민감하다고 말할 수 있습니다. 반대로 편향은 다른 훈련 데이터셋에서 여러 번 훈련했을 때 예측이 정확한 값에서 얼마나 벗어났는지 측정합니다. 편향은 무작위성이 아니라 구조적인 에러를 나타냅니다.
‘편향’과 ‘분산’ 용어의 기술적인 정의와 유도에 관심이 있다면 제 강의 노트를 참고하세요.
https://sebastianraschka.com/pdf/lecture-notes/stat479fs18/08_eval-intro_notes.pdf