3.4.1 최대 마진
큰 마진(large margin)의 결정 경계를 원하는 이유는 일반화 오차가 낮아지는 경향이 있기 때문입니다. 반면 작은 마진의 모델은 과대적합되기 쉽습니다. 마진 최대화를 이해하기 위해 결정 경계와 나란히 놓인 양성 샘플 쪽의 초평면과 음성 샘플 쪽의 초평면을 자세히 살펴보겠습니다. 이 두 초평면은 다음과 같이 쓸 수 있습니다.17
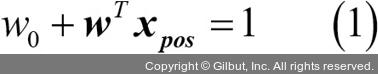
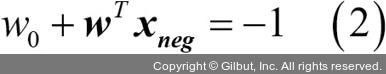
두 선형식 (1)과 (2)를 빼면 다음 결과를 얻습니다.
이 식을 다음과 같은 벡터 w의 길이로 정규할 수 있습니다.
결과 식은 다음과 같습니다.
이 식의 좌변은 양성 쪽 초평면과 음성 쪽 초평면 사이의 거리로 해석할 수 있습니다.18 이것이 최대화하려고 하는 마진(margin)입니다.
17 역주 여기서는 편의상 w0를 따로 표기했습니다. 이 식은 x2축과 만나는 절편을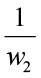 
만큼 위아래로 결정 경계와 나란하게 이동한 직선이 됩니다.
18 역주 직선 Ax + By + c = 0과 점 (x0, y0) 사이의 거리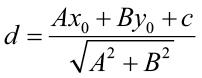 
이므로 왼쪽 식은 두 서포트 벡터 xpos와 xneg 사이의 거리가 됩니다.