이제 선형 SVM에 대한 기본 개념을 배웠습니다. 붓꽃 데이터셋의 꽃 분류 문제에 SVM 모델을 훈련해 보죠.
>>> from sklearn.svm import SVC
>>> svm = SVC(kernel='linear', C=1.0, random_state=1)
>>> svm.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std,
... y_combined,
... classifier=svm,
... test_idx=range(105, 150))
>>> plt.xlabel('petal length [standardized]')
>>> plt.ylabel('petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
앞 코드를 실행하면 그림 3-11과 같이 붓꽃 데이터셋에서 훈련한 SVM 분류기의 결정 영역 세 개가 나타납니다.22
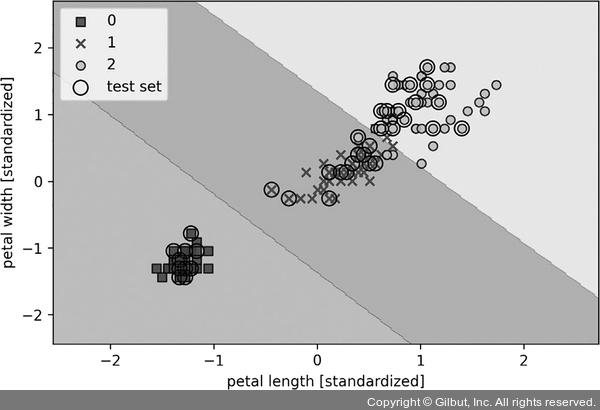
▲ 그림 3-11 SVM 분류기가 학습한 붓꽃 데이터셋의 결정 경계
Note ≡ 로지스틱 회귀 vs 서포트 벡터 머신
실제 분류 작업에서 선형 로지스틱 회귀와 선형 SVM은 종종 매우 비슷한 결과를 만듭니다. 로지스틱 회귀는 훈련 데이터의 조건부 가능도를 최대화하기 때문에 SVM보다 이상치에 민감합니다. SVM은 결정 경계에 가장 가까운 포인트(서포트 벡터)에 대부분 관심을 둡니다. 반면 로지스틱 회귀는 모델이 간단하고 구현하기가 더 쉬운 장점이 있습니다. 또 로지스틱 회귀 모델은 업데이트가 용이하므로 스트리밍 데이터를 다룰 때 적합합니다.
22 역주 svm 객체의 dual_coef_ 속성에서 서포트 벡터를 확인할 수 있습니다.