3.5.2 커널 기법을 사용하여 고차원 공간에서 분할 초평면 찾기
SVM으로 비선형 문제를 풀기 위해 매핑 함수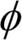 
를 사용하여 훈련 데이터를 고차원 특성 공간으로 변환합니다. 그다음 이 새로운 특성 공간에서 데이터를 분류하는 선형 SVM 모델을 훈련합니다. 동일한 매핑 함수 
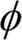를 사용하여 새로운 본 적 없는 데이터를 변환하고 선형 SVM 모델을 사용하여 분류할 수 있습니다.
이런 매핑 방식의 한 가지 문제점은 새로운 특성을 만드는 계산 비용이 매우 비싸다는 것입니다. 특히 고차원 데이터일 때 더욱 그렇습니다. 여기에 소위 커널 기법(kernel trick)이 등장하게 됩니다. SVM을 훈련하기 위해 콰드라틱 프로그래밍 문제를 어떻게 푸는지 상세히 다루지는 않겠습니다. 실전에서 필요한 것은 점곱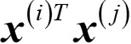 
를 
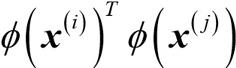로 바꾸는 것입니다. 두 포인트 사이 점곱을 계산하는 데 드는 높은 비용을 절감하기 위해 커널 함수(kernel function)를 정의합니다.
가장 널리 사용되는 커널 중 하나는 방사 기저 함수(Radial Basis Function, RBF)입니다. 가우시안 커널(Gaussian kernel)이라고도 합니다.25
간단하게 다음과 같이 쓰기도 합니다.
여기서 
은 최적화 대상 파라미터가 아닙니다.
25 역주 가우시안 커널을 사용하여 계산된 값은 지수 함수의 테일러 급수 전개를 생각하면 무한 차원의 다항식을 사용하여 만든 것으로 생각할 수 있습니다. 커널 방법은 이렇게 고차원 표현을 실제 만들지 않고 커널 함수의 계산 결과만 사용합니다. 고차원 표현을 명시적으로 만들지 않기 때문에 이 공간에 대한 결정 경계도 찾을 수 없습니다. 커널 방법을 사용할 때는 SVM의 목적 함수에 커널 함수를 적용하여 w와 b를 소거합니다. 이렇게 바뀐 목적 함수를 쌍대 형식(dual form)이라고 부릅니다. 예측은 새로운 데이터와 서포트 벡터에 커널 함수를 적용하여 계산합니다. SVC 클래스의 kernel 매개변수가 'linear'가 아닌 경우 항상 쌍대 문제가 되며 가중치 파라미터 coef_ 속성은 정의되지 않습니다. LinearSVC 클래스는 dual 매개변수의 기본값 True를 False로 바꾸어 쌍대 문제가 아니라 원 문제(primal problem)를 풀 수도 있습니다.