3.6.1 정보 이득 최대화: 자원을 최대로 활용

가장 정보가 풍부한 특성으로 노드를 나누기 위해 트리 알고리즘으로 최적화할 목적 함수를 정의합니다. 이 목적 함수는 각 분할에서 정보 이득을 최대화합니다. 정보 이득은 다음과 같이 정의합니다.

여기서 f는 분할에 사용할 특성입니다. D_p와 D_j는 부모와 j번째 자식 노드의 데이터셋입니다. I는 불순도(impurity) 지표입니다. N_p는 부모 노드에 있는 전체 샘플 개수입니다. N_j는 j번째 자식 노드에 있는 샘플 개수입니다. 여기서 볼 수 있듯이 정보 이득은 단순히 부모 노드의 불순도와 자식 노드의 불순도 합의 차이입니다. 자식 노드의 불순도가 낮을수록 정보 이득이 커집니다. 구현을 간단하게 하고 탐색 공간을 줄이기 위해 (사이킷런을 포함해서) 대부분의 라이브러리는 이진 결정 트리를 사용합니다. 즉, 부모 노드는 두 개의 자식 노드 D_left와 D_right로 나누어집니다.

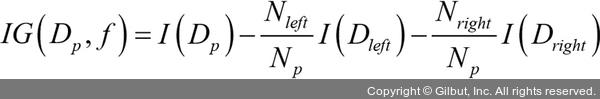
이진 결정 트리에 널리 사용되는 세 개의 불순도 지표 또는 분할 조건은 지니 불순도(Gini impurity, I_G), 엔트로피(entropy, I_H), 분류 오차(classification error, I_E)입니다. 샘플이 있는 모든 클래스()에 대한 엔트로피 정의는 다음과 같습니다.

여기서 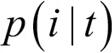는 특정 노드 t에서 클래스 i에 속한 샘플 비율입니다. 한 노드의 모든 샘플이 같은 클래스이면 엔트로피는 0이 됩니다. 클래스 분포가 균등하면 엔트로피는 최대가 됩니다. 예를 들어 이진 클래스일 경우 또는 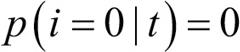이면 엔트로피는 0입니다. 클래스가 p(i = 1|t) = 0.5 와 p(i = 0|t) = 0.5 처럼 균등하게 분포되어 있으면 엔트로피는 1이 됩니다. 엔트로피 조건을 트리의 상호 의존 정보를 최대화하는 것으로 이해할 수 있습니다.²⁷