규제를 더 작은 가중치를 얻기 위해 비용 함수에 추가하는 페널티 항으로 생각할 수 있습니다. 다른 말로 하면 큰 가중치를 제한합니다. 규제 파라미터 λ로 규제의 강도를 크게 하면 가중치가 0에 가까워지고 훈련 데이터에 대한 모델 의존성은 줄어듭니다. L2 페널티 항에 대한 이 개념을 그림 4-5에 나타내 보죠.

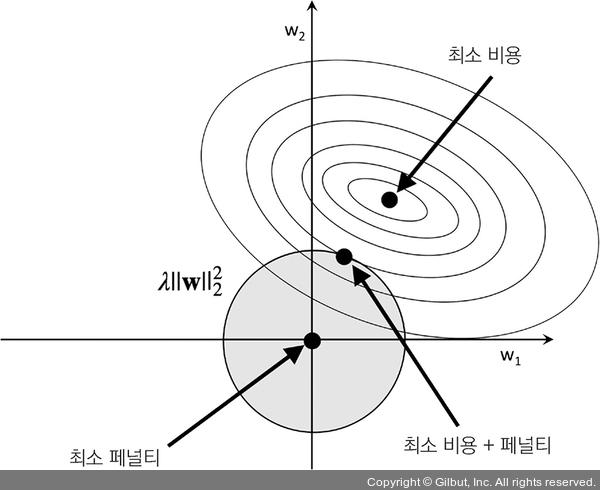
▲ 그림 4-5 L2 규제와 비용 함수

이차식인 L2 규제 항은 회색 공으로 표현되어 있습니다. 가중치 값은 규제 예산을 초과할 수 없습니다. 즉, 가중치 값의 조합이 회색 공 바깥에 놓일 수 없습니다. 반면 우리는 여전히 비용 함수를 최소화해야 합니다. 페널티 제약이 있는 상황에서 최선은 L2 회색 공과 규제가 없는 비용 함수의 등고선이 만나는 지점입니다. 규제 파라미터 λ가 커질수록 페널티 비용이 빠르게 증가하여 L2 공을 작게 만듭니다. 예를 들어 규제 파라미터를 무한대로 증가하면 가중치 값이 L2 공의 중심인 0이 될 것입니다. 이 예시에서 중요한 핵심을 정리하면 우리의 목표는 규제가 없는 비용과 페널티 항의 합을 최소화하는 것입니다. 이는 모델을 학습할 만한 충분한 훈련 데이터가 없을 때 편향을 추가하여 모델을 간단하게 만듦으로써 분산을 줄이는 것으로 해석할 수 있습니다.