공분산 행렬의 고유 벡터가 주성분(최대 분산의 방향)을 표현합니다.1 이에 대응되는 고윳값은 주성분의 크기입니다. Wine 데이터셋의 경우 13×13 차원의 공분산 행렬로부터 13개의 고유 벡터와 고윳값을 얻을 수 있습니다.
이제 세 번째 단계를 위해 공분산 행렬의 고유 벡터와 고윳값의 쌍을 구해 보죠. 선형대수학 수업의 기억을 떠올리면 고유 벡터 v는 다음 식을 만족합니다.2
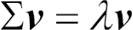
여기서 λ는 스케일을 담당하는 고윳값입니다. 고유 벡터와 고윳값을 직접 계산하는 것은 재미없고 복잡한 작업이기 때문에 넘파이의 linalg.eig 함수를 사용하여 Wine 데이터셋의 공분산 행렬에 대한 고유 벡터와 고윳값 쌍을 계산하겠습니다.3
>>> import numpy as np
>>> cov_mat = np.cov(X_train_std.T)
>>> eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
>>> print('\n고윳값 \n%s' % eigen_vals)
고윳값
[ 4.84274532 2.41602459 1.54845825 0.96120438 0.84166161 0.6620634 0.51828472
0.34650377 0.3131368 0.10754642 0.21357215 0.15362835 0.1808613 ]
numpy.cov 함수를 사용하여 표준화 전처리된 훈련 데이터셋의 공분산 행렬을 계산합니다. 그다음 linalg.eig 함수를 사용하여 고윳값 분해를 수행합니다. 이를 통해 13개의 고윳값이 들어 있는 벡터(eigen_vals)와 각 고윳값에 대응하는 고유 벡터가 열에 저장된 13×13 차원의 행렬(eigen_vecs)을 얻습니다.4
1 역주 원점에 중앙이 맞추어진 행렬 X가 있고 이 행렬의 주성분 벡터를 w라고 가정합니다. X를 w에 투영한 Xw의 분산이 최대가 되는 w를 찾으려 합니다. 분산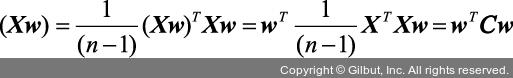 
처럼 공분산 행렬 C로 표현됩니다. 분산(Xw)을 λ로 놓으면 Cw = λw처럼 쓸 수 있습니다. 즉, 공분산 행렬의 가장 큰 고윳값(λ)에 해당하는 벡터 w를 찾는 문제가 됩니다.
2 역주 이 식의 Σ도 합 기호가 아니라 공분산 행렬을 나타냅니다.
3 역주 np.cov 함수는 특성이 열에 놓여 있을 것으로 기대하므로 훈련 데이터를 전치해서 전달합니다.
4 역주 13개의 고윳값 합은 1입니다. 고유 벡터는 원본 특성 공간에서 어떤 방향을 나타냅니다. 원본 데이터셋의 특성이 13개이므로 고유 벡터의 차원도 13입니다.